题目内容
18.先化简再求值:$\frac{m-2}{{m}^{2}-1}$÷(m-1-$\frac{2m-1}{m+1}$),其中m是方程x2-x=2016的解.分析 先将括号内通分计算分式的减法,再讲除式分子因式分解、除法转化为乘法,约分即可化简,由方程得解得概念可得m2-m=2016,即可知原式的值.
解答 解:原式=$\frac{m-2}{(m+1)(m-1)}$÷[$\frac{(m-1)^{2}(m+1)}{(m+1)(m-1)}$-$\frac{(2m-1)(m-1)}{(m+1)(m-1)}$]
=$\frac{m-2}{(m+1)(m-1)}$÷$\frac{(m-1)({m}^{2}-1-2m+1)}{(m+1)(m-1)}$
=$\frac{m-2}{(m+1)(m-1)}$•$\frac{(m+1)(m-1)}{(m-1)•m(m-2)}$
=$\frac{1}{{m}^{2}-m}$,
∵m是方程x2-x=2016的解,
∴m2-m=2016,
∴原式=$\frac{1}{2016}$.
点评 本题主要考查分式的化简与求值及方程得解的概念,熟练掌握分式的通分、约分及混合运算顺序化简分式是解题的关键.

练习册系列答案
相关题目
8.下列运算正确的是( )
| A. | -2x(3x2y-2xy)=-6x2y-4x2y | B. | 2x2y(-x2+2y+1)=-4x3y4 | ||
| C. | (3ab2-2ab)abc=3a2b2-2a2b2 | D. | (ab)2(2ab2c)=2a3b4c |
13.教师节来临,某校举办了以感恩为主题的贺卡制作比赛,赛后整理参赛学生的成绩,并制作成如表:
请根据如图表提供的信息解答下列问题:
(1)表中a、b、c所表示的数分别是:a=95,b=90,c=0.3;
(2)参赛学生比赛成绩的中位数落在哪个分数段?求出参赛学生成绩的平均得分;
(3)如果比赛成绩80分以上(含80分)可获得奖励,那么获奖率是多少?
| 分数段/分 | 组中值 | 频数(人数) | 频率 |
| 60≤x<70 | 65 | 30 | 0.15 |
| 70≤x<80 | 75 | b | 0.45 |
| 80≤x<90 | 85 | 60 | c |
| 90≤x<100 | a | 20 | 0.1 |
(1)表中a、b、c所表示的数分别是:a=95,b=90,c=0.3;
(2)参赛学生比赛成绩的中位数落在哪个分数段?求出参赛学生成绩的平均得分;
(3)如果比赛成绩80分以上(含80分)可获得奖励,那么获奖率是多少?
10.已知a>b,若c是任意实数,则下列不等式中总成立的是( )
| A. | a+c<b+c | B. | a-c>b-c | C. | ac<bc | D. | ac>bc |
7.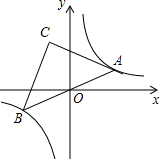 如图,点A是双曲线y=$\frac{8}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
如图,点A是双曲线y=$\frac{8}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
 如图,点A是双曲线y=$\frac{8}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
如图,点A是双曲线y=$\frac{8}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )| A. | y=$\frac{8}{x}$ | B. | y=$\frac{16}{x}$ | C. | y=-$\frac{16}{x}$ | D. | y=-$\frac{8}{x}$ |
8.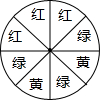 如图是一个可以自由转动的转盘,转动这个转盘后,转出( )色的可能性最小.
如图是一个可以自由转动的转盘,转动这个转盘后,转出( )色的可能性最小.
 如图是一个可以自由转动的转盘,转动这个转盘后,转出( )色的可能性最小.
如图是一个可以自由转动的转盘,转动这个转盘后,转出( )色的可能性最小.| A. | 红 | B. | 黄 | C. | 绿 | D. | 不确定 |
 如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连接CD,DE.
如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连接CD,DE.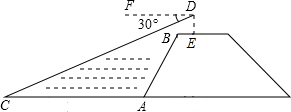 如图,小明站在河岸上的E点,看见正对面的河岸边有一点C,此时测得C点的俯角是30°.若小明的眼睛与地面的距离DE是1.6米,BE=1米,BE平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求河宽AC.(结果保留整数,参考数据:$\sqrt{3}$≈1.73)
如图,小明站在河岸上的E点,看见正对面的河岸边有一点C,此时测得C点的俯角是30°.若小明的眼睛与地面的距离DE是1.6米,BE=1米,BE平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求河宽AC.(结果保留整数,参考数据:$\sqrt{3}$≈1.73)