题目内容
10.如图1,在菱形ABCD中,∠BAD=60°,AB=2,E是DC边上一个动点,F是AB边上一点,∠AEF=30°.设DE=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图2所示,则这条线段可能是图中的( )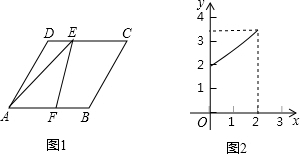
| A. | 线段EC | B. | 线段AE | C. | 线段EF | D. | 线段BF |
分析 求出当点E与点D重合时,即x=0时EC、AE、EF、BF的长可排除C、D;当点E与点C重合时,即x=2时,求出EC、AE的长可排除A,可得答案.
解答 解:当点E与点D重合时,即x=0时,EC=DC=2,AE=AD=2,
∵∠A=60°,∠AEF=30°,
∴∠AFD=90°,
在RT△ADF中,∵AD=2,
∴AF=$\frac{1}{2}$AD=1,EF=DF=ADcos∠ADF=$\sqrt{3}$,
∴BF=AB-AF=1,结合图象可知C、D错误;
当点E与点C重合时,即x=2时,
如图,连接BD交AC于H,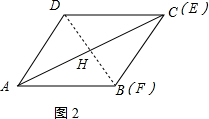
此时EC=0,故A错误;
∵四边形ABCD是菱形,∠BAD=60°,
∴∠DAC=30°,
∴AE=2AH=2ADcos∠DAC=2×2×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,故B正确.
故选:B.
点评 本题主要考查动点问题的函数图象与菱形的性质、解直角三角形的应用,结合函数图象上特殊点的实际意义排除法求解是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.一个角和它的余角的比是5:4,则这个角的补角是( )
| A. | 130° | B. | 50° | C. | 80° | D. | 100° |
18.已知等腰三角形的一边等于3,一边等于6,则它的周长为( )
| A. | 12 | B. | 12或15 | C. | 15 | D. | 15或18 |
19.若一元二次方程x2-2x-a=0无实数根,则一次函数y=(a+1)x+(a-1)不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.下列各方程中,是二元一次方程的是( )
| A. | 2x-1=1+x | B. | x+1=2xy | C. | $\frac{1}{x}+y=1$ | D. | x+2y-1=0 |
 如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.
如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.