题目内容
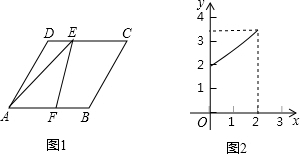
20. 如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.
如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.(1)你判断四边形ABEC形状是平行四边形;
(2)请你添加一个条件,使四边形ABEC是矩形,并请说明理由;
(3)当△ABC满足AB=AC条件时,四边形ABEC是菱形.(不需说理)
分析 (1)由将?ABCD的边DC延长到点E,使CE=DC,易得CE∥AB,CE=AB,即可判定四边形ABEC形状是平行四边形的性质;
(2)根据矩形的判定定理可得:可以添加AE=BC或∠ABE=90°等;
(3)根据菱形的判定定理可得:可以添加AB=AC或AE⊥BC等.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
即AB∥CE,
∵CE=DC,
∴AB=CE,
∴四边形ABEC是平行四边形;
故答案为:平行四边形;
(2)答案不唯一,如添加:AE=BC.
理由:∵四边形ABEC是平行四边形.AE=BC,
∴四边形ABEC是矩形(对角线相等的平行四边形是矩形);
(3)答案不唯一,如添加:AB=AC.
理由:∵四边形ABEC是平行四边形.AB=AC,
∴四边形ABEC是菱形(邻边相等的平行四边形是菱形).
故答案为:AB=AC.
点评 此题考查了矩形的判定、菱形的判定以及平行四边形的判定.注意熟记平行四边形、矩形、菱形的判定定理是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.若a<b,则下列各式中一定成立的是( )
| A. | -a<-b | B. | ac<bc | C. | a-1<b-1 | D. | $\frac{a}{3}$>$\frac{b}{3}$ |

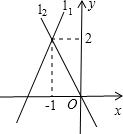 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x<k1x+b的解集为x>-1.
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x<k1x+b的解集为x>-1.