题目内容
18.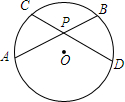 如图,已知⊙O的弦AB,CD相交于点P,PO平分∠APD,求证:AB=CD.
如图,已知⊙O的弦AB,CD相交于点P,PO平分∠APD,求证:AB=CD.
分析 作OE⊥AB于E,OF⊥CD于F,连结OA、OD、OP,如图,根据角平分线的性质得OE=OF,则利用勾股定理可得AE=DF,再根据垂径定理得到AE=BE,CF=DF,于是有AB=CD.
解答 证明:作OE⊥AB于E,OF⊥CD于F,连结OA、OD、OP,如图,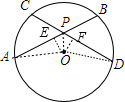
∵PO平分∠APD,
∴OE=OF,
在Rt△AOE中,AE=$\sqrt{O{A}^{2}-O{E}^{2}}$,
在Rt△ODF中,DF=$\sqrt{O{D}^{2}-O{F}^{2}}$,
而OA=OD,
∴AE=DF,
∵OE⊥AB,OF⊥CD,
∴AE=BE,CF=DF,
∴AB=CD.
点评 本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.本题的关键是作AB和CD的弦心距.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
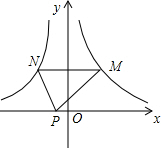 如图,点M是反比例函数y=$\frac{5}{x}$(x>0)图象上的一个动点,过点M作x轴的平行线交反比例函数y=-$\frac{5}{x}$(x<0)图象于点N.
如图,点M是反比例函数y=$\frac{5}{x}$(x>0)图象上的一个动点,过点M作x轴的平行线交反比例函数y=-$\frac{5}{x}$(x<0)图象于点N.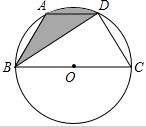 如图,已知点A、B、C、D均在已知圆上,AD∥BC,BD平分∠ABC,∠BAD=120°,四边形ABD的周长为15.
如图,已知点A、B、C、D均在已知圆上,AD∥BC,BD平分∠ABC,∠BAD=120°,四边形ABD的周长为15.