题目内容
4.某商场第一年初投入50万元进行商品经营,以后每年年终将当年获得的年利润与当年年初投入资金相加所得的总资金,作为下一年年初投入资金继续进行经营.(1)如果第一年的年利率为p,则第一年年终的总金可用代数式表示为50(1+p)万元.
(2)如果第二年的年获利率比第一年的年获利率多10个百分点,第二年年终的总资金为66万元,求第一年的年利率.
分析 (1)第一年年终的总资金=第一年初投入×(1+年获利率),依此列式计算即可求解;
(2)设第一年的年获利率为p,则第二年年终的总资金可表示为:50(1+p)(1+p+10%),根据题意可得方程,解方程后舍去不合题意的解,从而得出答案.
解答 解:(1)第一年年终的总资金为50(1+p)万元;
故答案为:50(1+p);
(2)设第一年的年获利率为p,依题意,得50(1+p)(1+p+0.1)=66,
整理,得p2+2.1p-0.22=0,
解得p1=0.1,p2=-2.2 (不合题意,舍去),
答:第一年利率为10%.
点评 此题主要考查了一元二次方程的应用,弄清题意,根据题目给出的条件,找出合适的等量关系,列出方程是解题的关键.

练习册系列答案
相关题目
16.计算$\frac{1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{199}-\frac{1}{200}}{\frac{1}{20{1}^{2}-{1}^{2}}+\frac{1}{20{2}^{2}-{2}^{2}}+…\frac{1}{30{0}^{2}-10{0}^{2}}}$的值为( )
| A. | 100 | B. | 200 | C. | 300 | D. | 400 |
13.(1)填表:
(2)根据你发现的规律填空:
①已知$\root{3}{3}=1.442$,则$\root{3}{3000}$=14.42,$\root{3}{0.003}$=0.1442.
②已知$\root{3}{0.000456}$=0.07696,则$\root{3}{456}$=0.7696.
| a | 0.000001 | 0.001 | 1 | 1000 | 1000000 |
| $\root{3}{a}$ | 0.01 | 0.1 | 1 | 10 | 100 |
①已知$\root{3}{3}=1.442$,则$\root{3}{3000}$=14.42,$\root{3}{0.003}$=0.1442.
②已知$\root{3}{0.000456}$=0.07696,则$\root{3}{456}$=0.7696.
 如图,点A(2,6)和点B(点B在点A的右侧)都在反比例函数的图象上,点C在y轴上,BC∥x轴,tan∠ACB=2,二次函数的图象经过A、B、C三点.
如图,点A(2,6)和点B(点B在点A的右侧)都在反比例函数的图象上,点C在y轴上,BC∥x轴,tan∠ACB=2,二次函数的图象经过A、B、C三点.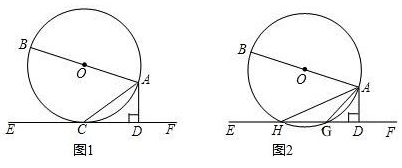
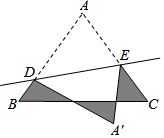 如图,等边△ABC的边长是5,D、E分别是边AB、AC上的点,将△ADE沿直线DE折叠,点A落在A′处,且点A′在△ABC外部,则阴影图形的周长为15.
如图,等边△ABC的边长是5,D、E分别是边AB、AC上的点,将△ADE沿直线DE折叠,点A落在A′处,且点A′在△ABC外部,则阴影图形的周长为15.
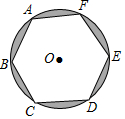 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为10;求图中阴影部分的面积.
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为10;求图中阴影部分的面积.