题目内容
一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或结论错误的是( )
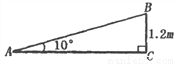
A. 斜坡AB的坡角是10° B. 斜坡AB的坡度是tan10° C. AC=1.2tan10°米 D. AB=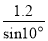 米
米
 C
【解析】根据题意及图形可知: 斜坡AB的坡角是10°,斜坡AB的坡度是tan10°, AC= 米, AB=米,
故错误的是C,
故选C.
C
【解析】根据题意及图形可知: 斜坡AB的坡角是10°,斜坡AB的坡度是tan10°, AC= 米, AB=米,
故错误的是C,
故选C.
练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
下列说法:①-3的绝对值是3;②-1的立方是-1;③ 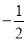 的相反数是-2;④-2的立方是-4.其中正确的是( )
的相反数是-2;④-2的立方是-4.其中正确的是( )
A. ①② B. ②③ C. ③④ D. ①④
 A
【解析】试题分析:①-3的绝对值是3,故正确;
②-1的立方是-1,故正确;
③的相反数是,故错误;
④-2的立方是-8,故错误.
所以正确的是①②.
故选A.
A
【解析】试题分析:①-3的绝对值是3,故正确;
②-1的立方是-1,故正确;
③的相反数是,故错误;
④-2的立方是-8,故错误.
所以正确的是①②.
故选A. 某商店举办有奖销售活动,办法如下:凡购物满100元者得奖券一张,多购多得,每10000张奖券为一个开奖单位,设立特等奖1个,一等奖50个,二等奖100个,那么买100元商品的中奖概率是( )
A. 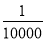 B.
B. 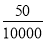 C.
C. 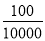 D.
D. 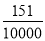
 D
【解析】每10000张奖券为一个开奖单位,共有奖:特等奖1个+一等奖50个+二等奖100个=151个奖,所以买100元商品的中奖的概率是,故选D.
D
【解析】每10000张奖券为一个开奖单位,共有奖:特等奖1个+一等奖50个+二等奖100个=151个奖,所以买100元商品的中奖的概率是,故选D. 在Rt△ABC中,∠C=90°,a=8,∠B=60°,解这个直角三角形.
 ∠A=30°,AB=16,AC=
【解析】试题分析:根据三角形内角和定理求出∠A,根据含30度角直角三角形求出AB,根据勾股定理求出AC即可.
试题解析:∵∠C=90°,∠B=60°,
∴∠A=180°-∠C-∠B=30°,
∵BC=a=8,
∴AB=2a=16,
由勾股定理得:AC= .
∠A=30°,AB=16,AC=
【解析】试题分析:根据三角形内角和定理求出∠A,根据含30度角直角三角形求出AB,根据勾股定理求出AC即可.
试题解析:∵∠C=90°,∠B=60°,
∴∠A=180°-∠C-∠B=30°,
∵BC=a=8,
∴AB=2a=16,
由勾股定理得:AC= . 如图,在△ABC 中,∠BAC=90°,AB=AC,点 D 为边AC 的中点,DE⊥BC 于点E,连接BD,则tan∠DBC 的值为 ( )
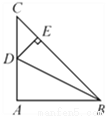
A. 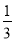 B.
B. 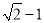 C.
C. 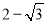 D.
D. 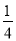
 A
【解析】试题分析:∵在△ABC中,∠BAC=Rt∠,AB=AC,∴∠ABC=∠C=45°,BC=AC,又∵点D为边AC的中点,∴AD=DC=AC,∵DE⊥BC于点E,∴∠CDE=∠C=45°,∴DE=EC=DC=AC,∴tan∠DBC===.故选A.
A
【解析】试题分析:∵在△ABC中,∠BAC=Rt∠,AB=AC,∴∠ABC=∠C=45°,BC=AC,又∵点D为边AC的中点,∴AD=DC=AC,∵DE⊥BC于点E,∴∠CDE=∠C=45°,∴DE=EC=DC=AC,∴tan∠DBC===.故选A. 如图,△ABC中,∠B=34°,∠ACB=104°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数.
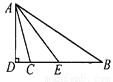
 35°.
【解析】由三角形的内角和定理,可求∠BAC=70°,又由AE是∠BAC的平分线,可求∠BAE=35°,再由AD是BC边上的高,可知∠ADB=90°,可求∠BAD=25°,所以∠DAE=∠BAE-∠BAD=10°.
【解析】
在△ABC中,
∵∠BAC=180°-∠B-∠C=70°,
∵AE是∠BAC的平分线,
∴∠BAE=∠CAE=35°.
又∵AD是BC边上的高,...
35°.
【解析】由三角形的内角和定理,可求∠BAC=70°,又由AE是∠BAC的平分线,可求∠BAE=35°,再由AD是BC边上的高,可知∠ADB=90°,可求∠BAD=25°,所以∠DAE=∠BAE-∠BAD=10°.
【解析】
在△ABC中,
∵∠BAC=180°-∠B-∠C=70°,
∵AE是∠BAC的平分线,
∴∠BAE=∠CAE=35°.
又∵AD是BC边上的高,... 如果将长度为a﹣2,a+5和a+2的三根线段首尾顺次相接可以得到一个三角形,那么a的取值范围是____________
 a>5
【解析】因为?2<2<5,所以a?2< a+2< a+5,
所以由三角形三边关系可得a?2+a+2>a+5,解得a>5.
a>5
【解析】因为?2<2<5,所以a?2< a+2< a+5,
所以由三角形三边关系可得a?2+a+2>a+5,解得a>5. 图中三角形的个数是( )
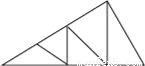
A. 8个 B. 9个 C. 10个 D. 11个
 B
【解析】试题解析:∵图中的三角形有:△AGD,△ADF,△AEF,△AEC,△ABC,△DGF,△DEF,△CEF,△CEB,
∴共9个三角形.
故选B.
B
【解析】试题解析:∵图中的三角形有:△AGD,△ADF,△AEF,△AEC,△ABC,△DGF,△DEF,△CEF,△CEB,
∴共9个三角形.
故选B. 如图,平面内有16个格点,每个格点小正方形的边长为1,则图中阴影部分的面积为__.
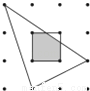
 【解析】试题解析:由题意,中间正方形中直角三角形的面积为,
∴阴影部分的面积为1-,
∴点P落在图中阴影部分的概率是.
【解析】试题解析:由题意,中间正方形中直角三角形的面积为,
∴阴影部分的面积为1-,
∴点P落在图中阴影部分的概率是. 
