题目内容
8.阅读下列材料:通过小学的学习我们知道,分数可分为“真分数”和“假分数”,而假分数都可化为常分数,如:$\frac{8}{3}$=$\frac{6+2}{3}$=2+$\frac{2}{3}$=2$\frac{2}{3}$.我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.如$\frac{x-1}{x+1}$,$\frac{{x}^{2}}{x-1}$这样的分式就是假分式;再如:$\frac{3}{x+1}$,$\frac{2x}{{x}^{2}+1}$这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).
如:$\frac{x-1}{x+1}$=$\frac{(x+1)-2}{x+1}$=1-$\frac{2}{x+1}$;
解决下列问题:
(1)分式$\frac{2}{x}$是真分式(填“真分式”或“假分式”);
(2)将假分式$\frac{{x}^{2}-1}{x+2}$化为带分式;
(3)如果x为整数,分式$\frac{2x-1}{x+1}$的值为整数,求所有符合条件的x的值.
分析 (1)利用题中的新定义判断即可;
(2)根据题中的方法把原式化为带分式即可;
(3)原式化为带分式,根据x与分式的值都为整数,求出x即可.
解答 解:(1)分式$\frac{2}{x}$是真分式;
故答案为:真;
(2)原式=$\frac{{x}^{2}+2x-2x-1}{x+2}$=x-$\frac{2x+1}{x+2}$=x-$\frac{2(x+2)-3}{x+2}$=x-2+$\frac{3}{x+2}$;
(3)原式=$\frac{2(x+1)-3}{x+1}$=2-$\frac{3}{x+1}$,
由x为整数,分式的值为整数,得到x+1=-1,-3,1,3,
解得:x=-2,-4,0,2,
则所有符合条件的x值为0,-2,2,-4.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.甲、乙两人沿同一个方向到同一个地点去,甲一半时间以速度a行走,另一半时间以速度b行走(b≠a);乙一半的路程以速度a行走,另一半路程以速度b行走,则先到达目的地的是( )
| A. | 甲 | B. | 乙 | C. | 同时到达 | D. | 与路程有关 |
17.在下列各组数中,三个数为勾股数的是( )
| A. | 2,3,4 | B. | 3,4,5 | C. | 4,5,6 | D. | 6,8,12 |
 如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式mx>kx+b>mx-4的解1<x<3.
如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式mx>kx+b>mx-4的解1<x<3.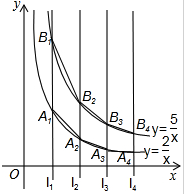 如图,直线l1:x=1,l2:x=2,l3:x=3,l4:x=4,…,与函数y=$\frac{2}{x}$(x>0)的图象分别交于点A1、A2、A3、A4、…;与函数y=$\frac{5}{x}$(x>0)的图象分别交于点B1、B2、B3、B4、…如果四边形A1A2B2B1的面积记为S1,四边形A2A3B3B2的面积记为S2,四边形A3A4B4B3的面积记为S3,…,以此类推,则S10的值是$\frac{63}{220}$.
如图,直线l1:x=1,l2:x=2,l3:x=3,l4:x=4,…,与函数y=$\frac{2}{x}$(x>0)的图象分别交于点A1、A2、A3、A4、…;与函数y=$\frac{5}{x}$(x>0)的图象分别交于点B1、B2、B3、B4、…如果四边形A1A2B2B1的面积记为S1,四边形A2A3B3B2的面积记为S2,四边形A3A4B4B3的面积记为S3,…,以此类推,则S10的值是$\frac{63}{220}$.