题目内容
16.菱形ABCD的周长为16,该菱形对角线的交点到AB边的距离为1,则∠DAB的度数为30或150度.分析 AC和BD相交于O点,OH⊥AB于H,OH=1,作DE⊥AB于E,如图,根据菱形的性质得AB∥CD,OB=OD,AD=4,则可判断OH为△BDE的中位线,所以DE=2OH=2,在Rt△AED中利用含30度的直角三角形三边的关系得∠ADE=30°,则利用平行线的性质有∠DAB=150°,当交换点A和点B的位置时,易得∠DAB=30°.
解答 解:AC和BD相交于O点,OH⊥AB于H,OH=1,
作DE⊥AB于E,如图,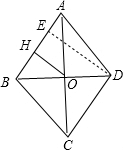
∵四边形ABCD为菱形,
∴AB∥CD,OB=OD,AD=4,
∴OH为△BDE的中位线,
∴DE=2OH=2,
在Rt△AED中,∵DE=$\frac{1}{2}$AD,
∴∠ADE=30°,
∴∠DAB=150°,
当交换点A和点B的位置时,则∠DAB=30°,
即∠DAB的度数为30°或150°.
故答案为30或150.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.

练习册系列答案
相关题目
4.下列四个数中,比0小的数是( )
| A. | 1 | B. | $\sqrt{3}$ | C. | π | D. | -1 |
11.春天是气温变化较大的季节,某地气象部门将2012年3月1日~6日和2013年3月1日~6日每天的最高气温统计如下表:
(1)分别求出2012年3月1日~6日和2013年3月1日~6日的平均气温和方差各是多少?
(2)利用(1)的结果,你来分析一下,2012年3月1日~6日和2013年3月1日~6日相比,哪个时间段的气温相对较高?哪个时间段的气温相对较稳定?
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 |
| 2012年3月 | 3℃ | 5℃ | 3℃ | 5℃ | 6℃ | 8℃ |
| 2013年3月 | 6℃ | 6℃ | 11℃ | 14℃ | 15℃ | 14℃ |
(2)利用(1)的结果,你来分析一下,2012年3月1日~6日和2013年3月1日~6日相比,哪个时间段的气温相对较高?哪个时间段的气温相对较稳定?
1.下列各式从左到右的变形中,属于因式分解的是( )
| A. | $\frac{1}{{x}^{2}}$-1=($\frac{1}{x}$+1)($\frac{1}{x}$-1) | B. | (a+b)2=a2+2ab+b2 | C. | x2-x-2=(x+1)(x-2) | D. | ax-ay-a=a(x-y)-1 |
5.点P为反比例函数y=$\frac{4}{x}$图象上一点,若P点的横坐标为2,则OP与x轴的正半轴夹角等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
6.下列计算正确的是( )
| A. | x2•x3=x6 | B. | (x2)3=x5 | C. | x5÷x3=x2 | D. | x2+x3=2x5 |
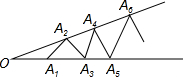 如图,已知点A1、A2、A3、A4…是∠O两边上的点,且O A1=A1 A2=A2 A3=A3 A4=A4 A5=…,从左向右数,恰好只能作出4个等腰三角形,请问∠O=18°.
如图,已知点A1、A2、A3、A4…是∠O两边上的点,且O A1=A1 A2=A2 A3=A3 A4=A4 A5=…,从左向右数,恰好只能作出4个等腰三角形,请问∠O=18°.