题目内容
 如图,菱形ABCD中,CF⊥AD垂足为E,交BD的延长线于F,求证:AO2=BO•OF.
如图,菱形ABCD中,CF⊥AD垂足为E,交BD的延长线于F,求证:AO2=BO•OF.考点:菱形的性质,相似三角形的判定与性质
专题:证明题
分析:运用菱形的性质证明∠F=∠DCO,此为解决该题的关键结论;证明△DOC∽△COF,结合BO=DO,AO=CO,即可解决问题.
解答: 解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,
∴DO⊥CO,AO=CO;DA=DC,
∴∠DAC=∠DCA;
∵CF⊥AD,
∴∠F+∠ECA=∠DAC+∠ECA,
∴∠F=∠DAC;而∠DAC=∠DCA,
∴∠F=∠DCO;而∠DOC=∠COF,
∴△DOC∽△COF,
∴CO:FO=DO:CO,而BO=DO,AO=CO,
∴AO2=BO•OF.
 解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,∴DO⊥CO,AO=CO;DA=DC,
∴∠DAC=∠DCA;
∵CF⊥AD,
∴∠F+∠ECA=∠DAC+∠ECA,
∴∠F=∠DAC;而∠DAC=∠DCA,
∴∠F=∠DCO;而∠DOC=∠COF,
∴△DOC∽△COF,
∴CO:FO=DO:CO,而BO=DO,AO=CO,
∴AO2=BO•OF.
点评:该题主要考查了菱形的性质、相似三角形的判定及其性质等几何知识点的应用问题;深入把握题意,大胆猜测推理、科学求解论证是解题的关键.

练习册系列答案
相关题目
等腰三角形一边长等于5,一边长等于9,则它的周长是( )
| A、14 | B、23 |
| C、19 | D、19或23 |
若|x-
|+|2y+1|=0,则x2+y2的值是( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题.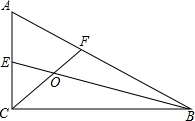 如图,∠ACB=90°,∠ABC=30°,BE、CF分别平分∠ABC、∠ACB,交AC、AB于点E、F,BE,CF交于点O,求证:OE=OF.
如图,∠ACB=90°,∠ABC=30°,BE、CF分别平分∠ABC、∠ACB,交AC、AB于点E、F,BE,CF交于点O,求证:OE=OF. 如图,AC平分∠BAD,其中∠B=50°,∠ADC=80°,求∠BAC、∠ACD的度数.
如图,AC平分∠BAD,其中∠B=50°,∠ADC=80°,求∠BAC、∠ACD的度数.