题目内容
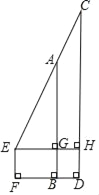
【题目】如图,左、右并排的两棵树AB和CD,小树的高AB=6m,大树的高CD=9m,小明估计自己眼睛距地面EF=1.5m,当他站在F点时恰好看到大树顶端C点.已知此时他与小树的距离BF=2m,则两棵树之间的距离BD是( )
A. 1m B. ![]() m C. 3m D.
m C. 3m D. ![]() m
m
【答案】B
【解析】
由∠AGE=∠CHE=90°,∠AEG=∠CEH可证明△AEG∽△CEH,根据相似三角形对应边成比例求出GH的长即BD的长即可.
由题意得:FB=EG=2m,AG=AB﹣BG=6﹣1.5=4.5m,CH=CD﹣DH=9﹣1.5=7.5m,
∵AG⊥EH,CH⊥EH,
∴∠AGE=∠CHE=90°,
∵∠AEG=∠CEH,
∴△AEG∽△CEH,
∴ ![]() =
=![]() =
=![]() ,即
,即 ![]() =
=![]() ,
,
解得:GH=![]() ,
,
则BD=GH=![]() m,
m,
故选:B.

练习册系列答案
相关题目
【题目】为让家园更美丽,我市今年进一步推进全国文明城市、 国家卫生城市的创建工作,学校把“双创”工作推向深入,组织了以文明卫生知识竞赛,每班派相同人数的学生参加,成绩分别为![]() 四个等级.其中相应等级的得分依次记为
四个等级.其中相应等级的得分依次记为![]() 分、
分、![]() 分、
分、![]() 分、
分、![]() 分,学校将八年级的一班和二班的成绩整理并绘制成如下统计图表:
分,学校将八年级的一班和二班的成绩整理并绘制成如下统计图表: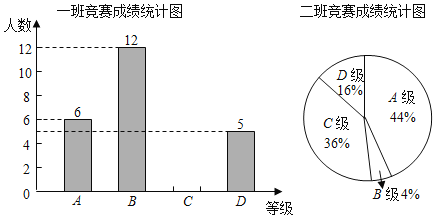
班级 | 平均数(分) | 中位数(分) | 众数(分) |
一班 |
|
|
|
二班 |
|
|
|
根据以上提供的信息解答下列问题:
(1)请补全一班竞赛成绩统计图;
(2)请直接写出![]() 的值;
的值;
(3)你认为哪个班成绩较好,诸写出支持你观点的理由.