��Ŀ����
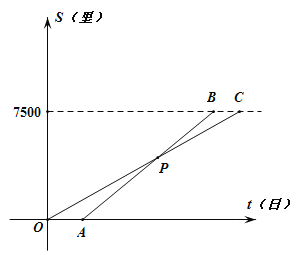
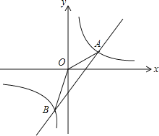
����Ŀ���Ķ��龳�����ۺ�ʵ�����ϣ�ͬѧ��̽����ȫ�ȵĵ���ֱ��������ͼ�α仯������
��ͼ1��![]() ������
������![]() ��
��![]() ����ʱ����
����ʱ����![]() ���
���![]() �غϣ�
�غϣ�
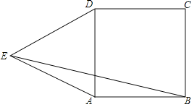
����̽��1:��1��С����ͼ1�е�����ȫ�ȵ�![]() ��
��![]() ��ͼ2��ʽ�ڷţ���
��ͼ2��ʽ�ڷţ���![]() ����
����![]() �ϣ�
�ϣ�![]() ����ֱ�߽�
����ֱ�߽�![]() ����ֱ���ڵ�
����ֱ���ڵ�![]() ������
������![]() ����֤��
����֤��![]() ��
��
����̽��2:��2��С��ͼ1�е�![]() �Ƶ�
�Ƶ�![]() ����ʱ�뷽����ת�Ƕ�
����ʱ�뷽����ת�Ƕ�![]()
![]() ��Ȼ�ֱ��ӳ�
��Ȼ�ֱ��ӳ�![]() ��
��![]() �������ཻ�ڵ�
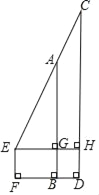
�������ཻ�ڵ�![]() ����ͼ3���ڲ����У�С������������⣬������
����ͼ3���ڲ����У�С������������⣬������
��![]() ʱ����֤��
ʱ����֤��![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�
�ڵ�![]() __________ʱ��
__________ʱ��![]() ����ֱ�ӻشɣ�
����ֱ�ӻشɣ�
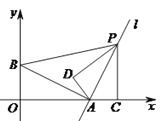
����̽��3:��3��Сӱ��ͼ1�е�![]() �Ƶ�
�Ƶ�![]() ��˳ʱ�뷽����ת�Ƕ�
��˳ʱ�뷽����ת�Ƕ�![]()
![]() ���߶�
���߶�![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ���ڲ����У�Сӱ����������⣬������
���ڲ����У�Сӱ����������⣬������
����ͼ4����![]() ʱ��ֱ��д���߶�
ʱ��ֱ��д���߶�![]() �ij�Ϊ_________��
�ij�Ϊ_________��
����ͼ5������ת����![]() �DZ�
�DZ�![]() ���е�ʱ��ֱ��д���߶�
���е�ʱ��ֱ��д���߶�![]() �ij�Ϊ____________��
�ij�Ϊ____________��
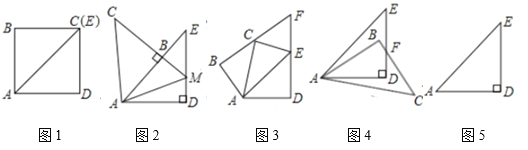
���𰸡���1������������2���ټ���������![]() ����3����
����3����![]() ����
����![]()
��������
��1��֤��Rt��AMB��Rt��AMD���ɽ�����⣮
��2����֤����FCE=��FEC=60�����ɽ�����⣮
�ڸ���ƽ���ߵ��ж��������ɽ�����⣮
��3��������EC��֤����AEC�ǵȱ������Σ����ù��ɶ������AE���ɽ�����⣮
����ͼ5�У�����AF��BD���ڵ�O������֤��EC=BD����֤��OB=OD��������������OB���ɽ�����⣮
��1��֤������ͼ2��

![]() ��
��![]() ��
��![]() ��
��
![]()
![]() ��
��
![]() ��
��
��2����֤������ͼ3�У�

![]() ��
��![]() ��
��
![]()
![]() ��
��![]()
![]() ��
��
![]() ��
��
![]() ��
��
![]() �ǵȱ������Σ�
�ǵȱ������Σ�
���⣺��![]() ʱ��
ʱ��![]() ���������£�
���������£�
��![]() ��
��
��![]() ��
��
![]() ��
��
��![]() ��
��
![]() ��
��![]() ʱ��
ʱ��![]() ��
��
�ʴ�Ϊ![]() ��
��
��3�����⣺��ͼ4�У�����![]() ,
,

![]() ��
��![]() ��
��
![]() �ǵȱ������Σ�
�ǵȱ������Σ�
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
�ʴ�Ϊ![]() ��
��
���⣺��ͼ5�У�����![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��

![]() ��
��![]() ��
��![]() ��
��
![]()
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]()
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��ֱƽ���߶�
��ֱƽ���߶�![]() ��
��
![]() ��
��
��![]() ��
�У�
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
�ʴ�Ϊ![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�