题目内容
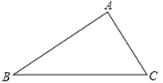
【题目】如图，△ABC内接于⊙O，AD是△ABC的中线，AE∥BC，射线BE交AD于点F，交⊙O于点G，点F是BE的中点，连接CE．
（1）求证：四边形ADCE为平行四边形；
（2）若BC=2AB，求证: 
．
【答案】（1）证明见解析；（2）证明见解析；
【解析】
（1）根据三角形中位线的性质和平行四边形的判定证明即可；
（2）根据平行四边形的性质和等腰三角形的性质解答即可．
（1）∵AD是△ABC的中线，
∴D是BC的中点，
∵F是BE的中点，
∴DF是△BCE的中位线，
∴DF∥CE，
∴AD∥CE，
∵AE∥BC，
∴四边形ADCE是平行四边形；
（2）∵四边形ADCE是平行四边形，
∴AE=CD，
∵AD是△ABC的中线，
∴BC=2CD，
∴BC=2AE，
∵BC=2AB，
∴AB=AE，
∴∠ABE=∠AEB，
∵AE∥BC，
∴∠AEB=∠DBE，
∴∠ABE=∠DBE，
∴
．
练习册系列答案
相关题目
