Question

【题目】若顺次连接四边形ABCD四边中点所得的四边形是矩形，则原四边形的对角线AC、BD所满足的条件是_____．

Answer 1

【答案】AC⊥BD

【解析】

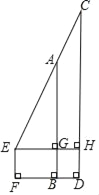
根据题意画出相应的图形，如图所示，由四边形EFGH为矩形，根据矩形的四个角为直角得到∠FEH=90°，又EF为三角形ABD的中位线，根据中位线定理得到EF与DB平行，根据两直线平行，同旁内角互补得到∠EMO=90°，同理根据三角形中位线定理得到EH与AC平行，再根据两直线平行，同旁内角互补得到∠AOD=90°，根据垂直定义得到AC与BD垂直．

∵四边形EFGH是矩形，

∴∠FEH=90°，

又∵点E、F、分别是AD、AB、各边的中点，

∴EF是三角形ABD的中位线，

∴EF∥BD，

∴∠FEH=∠OMH=90°，

又∵点E、H分别是AD、CD各边的中点，

∴EH是三角形ACD的中位线，

∴EH∥AC，

∴∠OMH=∠COB=90°，

即AC⊥BD．

故答案为：AC⊥BD．