题目内容
13.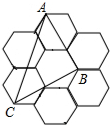 如图,由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )
如图,由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3$\sqrt{3}$ |
分析 延长AB,然后作出过点C与格点所在的直线,一定交于格点E,根据S△ABC=S△AEC-S△BEC即可求解.
解答 解:延长AB,然后作出过点C与格点所在的直线,一定交于格点E.如图所示:
正六边形的边长为1,则半径是1,则CE=4,
两平行的边之间距离是:$\sqrt{3}$,
则△BCE的边EC上的高是:$\sqrt{3}$,
△ACE边EC上的高是:$\frac{5}{2}$$\sqrt{3}$,
则S△ABC=S△AEC-S△BEC=$\frac{1}{2}$×4×($\frac{5}{2}$$\sqrt{3}$-$\sqrt{3}$)=3$\sqrt{3}$.
故选:D.
点评 本题考查了正六边形的性质、正多边形的计算;正确理解S△ABC=S△AEC-S△BEC是关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
8.在-3.14,$\frac{22}{7}$,0,π中,有理数有( )个.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |