题目内容
1.计算(-2015)0+(${\frac{1}{3}$)-2的结果是10.分析 首先根据非零数的零次幂等于1,可得(-2015)0=1;然后根据负整数指数幂的运算方法,求出(${\frac{1}{3}$)-2的值是多少;最后把(-2015)0、(${\frac{1}{3}$)-2的值相加,求出(-2015)0+(${\frac{1}{3}$)-2的结果是多少即可.
解答 解:∵(-2015)0+(${\frac{1}{3}$)-2=1+9=10,
∴计算(-2015)0+(${\frac{1}{3}$)-2的结果是10.
故答案为:10.
点评 (1)此题主要考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.
(2)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a0=1(a≠0);②00≠1.

练习册系列答案
相关题目
9.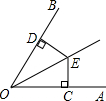 如图,OE平分∠AOB,EC⊥OA于点C,ED⊥OB于点D,ED与EC的长度关系为( )
如图,OE平分∠AOB,EC⊥OA于点C,ED⊥OB于点D,ED与EC的长度关系为( )
 如图,OE平分∠AOB,EC⊥OA于点C,ED⊥OB于点D,ED与EC的长度关系为( )
如图,OE平分∠AOB,EC⊥OA于点C,ED⊥OB于点D,ED与EC的长度关系为( )| A. | ED>EC | B. | ED=EC | C. | ED<EC | D. | 无法确定 |
13.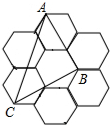 如图,由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )
如图,由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )
 如图,由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )
如图,由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3$\sqrt{3}$ |
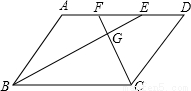
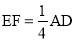 ,那么平行四边形ABCD应满足的条件是【 】
,那么平行四边形ABCD应满足的条件是【 】