题目内容
3.①(2x+1)2=2(2x+1)②用配方法解方程x2-6x-7=0
③($\sqrt{\frac{1}{8}}-\sqrt{48}$)-($\sqrt{0.5}-2\sqrt{\frac{1}{3}}-\sqrt{32}$)
④2a$\sqrt{{3a{b^2}}}-\frac{b}{2}\sqrt{27{a^3}}+3ab\sqrt{\frac{1}{3}a}$
⑤($\sqrt{5}-\sqrt{3}+\sqrt{2}$)($\sqrt{5}+\sqrt{3}-\sqrt{2}$)
⑥tan60°+4sin245°-2cos30°.
分析 (1)根据一元二次方程的解法解答即可;
(2)根据配方法解一元二次方程即可;
(3)根据二次根式的混合计算解答即可;
(4)根据二次根式的混合计算解答即可;
(5)根据二次根式的混合计算解答即可;
(6)根据三角函数进行解答即可.
解答 解:①(2x+1)(2x+1-2)=0,
2x+1=0或2x-1=0,
${x_1}=-\frac{1}{2}$,${x_2}=\frac{1}{2}$;
②(x-3)2=16
x-3=±4
x1=7,x2=-1;
③原式=$\frac{1}{4}\sqrt{2}-4\sqrt{3}-\frac{1}{2}\sqrt{2}+\frac{2}{3}\sqrt{3}+4\sqrt{2}$
=($\frac{1}{4}-\frac{1}{2}+4$)$\sqrt{2}$+(-4+$\frac{2}{3}$)$\sqrt{3}$
=$\frac{15}{4}\sqrt{2}-\frac{10}{3}\sqrt{3}$;
④原式=2$ab\sqrt{3a}-\frac{3ab}{2}\sqrt{3a}+ab\sqrt{3a}$
=(2-$\frac{3}{2}+1$)$ab\sqrt{3a}$
=$\frac{3}{2}ab\sqrt{3a}$;
⑤原式=${(\sqrt{5})^2}-{(\sqrt{3}-\sqrt{2})^2}$
=5-(3-2$\sqrt{6}$+2)
=5-3+2$\sqrt{6}$-2
=2$\sqrt{6}$;
⑥原式=$\sqrt{3}$+4×($\frac{{\sqrt{2}}}{2}$)2-2×$\frac{{\sqrt{3}}}{2}$
=$\sqrt{3}+2-\sqrt{3}$
=2.
点评 此题考查实数的混合计算,关键是根据一元二次方程、二次根式和三角函数进行解答.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 30% | B. | 25% | C. | 20% | D. | 15% |
| A. | 点P在⊙O内 | B. | 点P在⊙O上 | C. | 点P在⊙O外 | D. | 无法确定 |
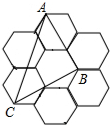 如图,由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )
如图,由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3$\sqrt{3}$ |
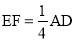 ,那么平行四边形ABCD应满足的条件是【 】
,那么平行四边形ABCD应满足的条件是【 】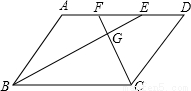
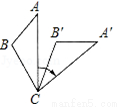
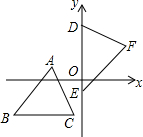 如图,坐标平面上,△ABC≌△FDE,若A点的坐标为(a,1),BC∥x轴,B点的坐标为(b,-3),D、E两点在y轴上,则F点到y轴的距离为4.
如图,坐标平面上,△ABC≌△FDE,若A点的坐标为(a,1),BC∥x轴,B点的坐标为(b,-3),D、E两点在y轴上,则F点到y轴的距离为4.