��Ŀ����
3��С����С����һ����Ϸ��С�������������˿��Ʒֱ���3��4��5��С���������˿���6��7���ֶ��˸����Լ�����ϴ�ȣ�С����С������������ȡһ�ţ�С���С�������������ȡһ�ţ�������������֮�ͣ������Ϊ��������С��ʤ�������Ϊż����С��ʤ����1�����б�����״ͼ�ķ������г�С����С���õ�����֮�����п��ܳ��ֵ������
��2�����жϸ���Ϸ��˫���Ƿ�ƽ����˵�����ɣ�
���� ��1���������⻭����״ͼ��Ȼ����ݸ��ʹ�ʽ��ʽ���м��㼴�ɵý⣻
��2�����ݼ�����ʱȽϼ��ɣ�
��� �⣺��1��������״ͼ���£�
��2������Ϸ��ƽ��������ͼ��֪��С��Ӯ�ĸ���=$\frac{1}{2}$=С��Ӯ�ĸ��ʣ�
���� ���⿼�������б�������״ͼ������ʣ��õ���֪ʶ��Ϊ������=������������������֮�ȣ�

��ϰ��ϵ�д�
�����Ŀ
13��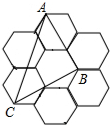 ��ͼ����7����״����С��ȫ��ͬ������������ɵ������������εĶ����Ϊ��㣬��֪ÿ���������εı߳�Ϊ1����ABC�Ķ��㶼�ڸ���ϣ����ABC������ǣ�������
��ͼ����7����״����С��ȫ��ͬ������������ɵ������������εĶ����Ϊ��㣬��֪ÿ���������εı߳�Ϊ1����ABC�Ķ��㶼�ڸ���ϣ����ABC������ǣ�������
 ��ͼ����7����״����С��ȫ��ͬ������������ɵ������������εĶ����Ϊ��㣬��֪ÿ���������εı߳�Ϊ1����ABC�Ķ��㶼�ڸ���ϣ����ABC������ǣ�������
��ͼ����7����״����С��ȫ��ͬ������������ɵ������������εĶ����Ϊ��㣬��֪ÿ���������εı߳�Ϊ1����ABC�Ķ��㶼�ڸ���ϣ����ABC������ǣ�������| A�� | $\sqrt{2}$ | B�� | 2$\sqrt{3}$ | C�� | 3$\sqrt{2}$ | D�� | 3$\sqrt{3}$ |
13������˵����ȷ���ǣ�������
| A�� | ����ʽ2x+3x2+1�Ƕ�������ʽ | B�� | ����ʽa��ϵ����0��������0 | ||
| C�� | $\frac{xy-1}{2}$�Ƕ��ε���ʽ | D�� | ����ʽ-$\frac{2}{5}$x2y��ϵ����-2��������2 |
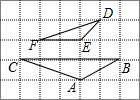 ��ͼ��������������ÿ��С�����εı߳�Ϊ1����ABC�͡�EDF�ĵ㶼������ĸ���ϣ�
��ͼ��������������ÿ��С�����εı߳�Ϊ1����ABC�͡�EDF�ĵ㶼������ĸ���ϣ� ��ͼ����P�ں���y=-x��ͼ�����˶�����A������Ϊ��1��0�������߶�AP���ʱ����P������Ϊ��$\frac{1}{2}��-\frac{1}{2}$����
��ͼ����P�ں���y=-x��ͼ�����˶�����A������Ϊ��1��0�������߶�AP���ʱ����P������Ϊ��$\frac{1}{2}��-\frac{1}{2}$����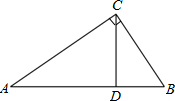 ��ͼ����Rt��ABC�У���ACB=90�㣬CD�DZ�AB�ϵĸߣ�
��ͼ����Rt��ABC�У���ACB=90�㣬CD�DZ�AB�ϵĸߣ�