题目内容
 如图,在平面直角坐标系中,点A(-2,0)点B(0,4),OB的垂直平分线 CE与OA的垂直平分线CD相交于点C,现存在点F,会使得△CDF≌△0AB,写出点F的坐标
如图,在平面直角坐标系中,点A(-2,0)点B(0,4),OB的垂直平分线 CE与OA的垂直平分线CD相交于点C,现存在点F,会使得△CDF≌△0AB,写出点F的坐标考点:全等三角形的判定,坐标与图形性质
专题:
分析:根据点A、B的坐标求出OA、OB的长,再根据线段垂直平分线的定义求出OD、OE的长,然后判断出四边形CDOE是矩形,然后写出点C的坐标,分:①点C是直角顶点时,根据全等三角形对应边相等可得CF=OB;②点D是直角顶点,根据全等三角形对应边相等可得DF=OB;然后分别分两种情况写出点F的坐标即可.
解答:解:∵点A(-2,0)点B(0,4),
∴OA=2,OB=4,
∵OB的垂直平分线CE,与OA的垂直平分线CD相交于点C,
∴OD=
OA=
×2=1,OE=
OB=
×4=2,
∴点C(-1,2),
①点C是直角顶点时,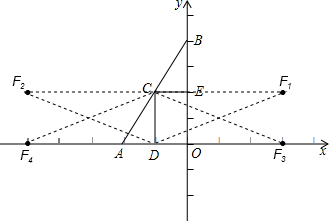
如图,∵△CDF≌△0AB,
∴CF=OB=4,
点F在CD右边时,F1(3,2),
点F在CD左边时,F2(-5,2);
②点D是直角顶点时,
∵△CDF≌△A0B,
∴DF=OB=4,
点F在CD右边时,F3(3,0),
点F在CD左边时,F4(-5,0);
综上所述,存在点F1(3,2),F2(-5,2),F3(3,0),F4(-5,0),使得△CDF≌△0AB.
故答案为:(3,2),(-5,2),(3,0),(-5,0).
∴OA=2,OB=4,
∵OB的垂直平分线CE,与OA的垂直平分线CD相交于点C,
∴OD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴点C(-1,2),
①点C是直角顶点时,

如图,∵△CDF≌△0AB,
∴CF=OB=4,
点F在CD右边时,F1(3,2),
点F在CD左边时,F2(-5,2);
②点D是直角顶点时,
∵△CDF≌△A0B,
∴DF=OB=4,
点F在CD右边时,F3(3,0),
点F在CD左边时,F4(-5,0);
综上所述,存在点F1(3,2),F2(-5,2),F3(3,0),F4(-5,0),使得△CDF≌△0AB.
故答案为:(3,2),(-5,2),(3,0),(-5,0).
点评:本题考查了全等三角形的判定与性质,线段垂直平分线的性质,坐标与图形,难点在于要分情况讨论,作出图形更形象直观.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
下列合并同类项正确的是( )
| A、3x+y=4xy |
| B、2x2+3x2=5x4 |
| C、6x2-3x2=3 |
| D、5xy-3xy=2xy |
已知一个圆锥的侧面展开图的圆心角为180°,且它的母线长为4cm,那么它的底面圆半径为( )
A、
| ||
| B、1cm | ||
C、
| ||
| D、2cm |

 已知在△ABC中,BD平分∠ABC,EF垂直平分BD,交CA的延长线于点E,求证:∠EAB=∠EBC.
已知在△ABC中,BD平分∠ABC,EF垂直平分BD,交CA的延长线于点E,求证:∠EAB=∠EBC.