题目内容
3. 如图,二次函数y=-x2+3x+m的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点
如图,二次函数y=-x2+3x+m的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点(1)求m的值及C点坐标;
(2)在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大,若存在,求出此时M点坐标;若不存在,请简要说明理由
(3)P为抛物线上一点,它关于直线BC的对称点为Q
①当四边形PBQC为菱形时,求点P的坐标;
②点P的横坐标为t(0<t<4),当t为何值时,四边形PBQC的面积最大,请说明理由.
分析 (1)用待定系数法求出抛物线解析式;
(2)先判断出面积最大时,平移直线BC的直线和抛物线只有一个交点,从而求出点M坐标;
(3)①先判断出四边形PBQC时菱形时,点P是线段BC的垂直平分线,利用该特殊性建立方程求解;
②先求出四边形PBCQ的面积与t的函数关系式,从而确定出它的最大值.
解答 解:(1)将B(4,0)代入y=-x2+3x+m,
解得,m=4,
∴二次函数解析式为y=-x2+3x+4,
令x=0,得y=4,
∴C(0,4),
(2)存在,
理由:∵B(4,0),C(0,4),
∴直线BC解析式为y=-x+4,
当直线BC向上平移b单位后和抛物线只有一个公共点时,△MBC面积最大,
∴$\left\{\begin{array}{l}{y=-x+4+b}\\{y=-{x}^{2}+3x+4}\end{array}\right.$,
∴x2-4x+b=0,
∴△=16-4b=0,
∴b=4,
∴$\left\{\begin{array}{l}{x=2}\\{y=6}\end{array}\right.$,
∴M(2,6),
(3)①如图,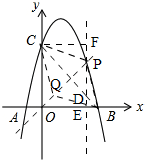
∵点P在抛物线上,
∴设P(m,-m2+3m+4),
当四边形PBQC是菱形时,点P在线段BC的垂直平分线上,
∵B(4,0),C(0,4)
∴线段BC的垂直平分线的解析式为y=x,
∴m=-m2+3m+4,
∴m=1±$\sqrt{5}$,
∴P(1+$\sqrt{5}$,1+$\sqrt{5}$)或P(1-$\sqrt{5}$,1-$\sqrt{5}$),
②如图,
设点P(t,-t2+3t+4),
过点P作y轴的平行线l,过点C作l的垂线,
∵点D在直线BC上,
∴D(t,-t+4),
∵PD=-t2+3t+4-(-t+4)=-t2+4t,
BE+CF=4,
∴S四边形PBQC=2S△PCB=2(S△PCD+S△PBD)=2($\frac{1}{2}$PD×CF+$\frac{1}{2}$PD×BE)=4PD=-4t2+16t,
∵0<t<4,
∴当t=2时,S四边形PBQC最大=16
点评 此题是二次函数综合题,主要考查了待定系数法,极值的确定,对称性,面积的确定,解本题的关键是确定出△MBC面积最大时,点P的坐标.

| A. | 东经118°,北纬40° | B. | 微山县文化街 | ||
| C. | 北偏东60° | D. | 望湖楼电影院3排 |

| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
| A. | 3 | B. | 2 | C. | -2 | D. | 2或-2 |
| A. | a | B. | a+3 | C. | $\frac{5}{6}$a | D. | a+15 |
| A. | (0,-6) | B. | (-6,0) | C. | (3,0) | D. | (0,3) |
| A. | a=6,b=8,c=10 | B. | a=5,b=12,c=13 | C. | a=1,b=2,c=3 | D. | a=3,b=4,c=5 |
 如图,将面积为9的△ABC沿BC方向平移2个单位得到△A1B1C1,若B1C=4,则△A1B1C1的底边B1C1上的高为3.
如图,将面积为9的△ABC沿BC方向平移2个单位得到△A1B1C1,若B1C=4,则△A1B1C1的底边B1C1上的高为3.