题目内容
2. 如图,已知菱形ABCD的两条对角线长分别为12和16,M、N分别是边BC、CD的中点,P是对角线BD上一动点,则PM+PN的最小值为10.
如图,已知菱形ABCD的两条对角线长分别为12和16,M、N分别是边BC、CD的中点,P是对角线BD上一动点,则PM+PN的最小值为10.
分析 要求PM+PN的最小值,PM、PN不能直接求,可考虑通过作辅助线转化PN、PM的值,从而找出其最小值求解.
解答 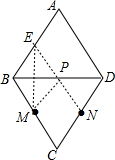 解:如图:
解:如图:
作ME⊥BD交AB于E,连接EN,
则EN就是PM+PN的最小值,
∵四边形ABCD是菱形,
∴AB=CD,
∵M、N分别是边BC、CD的中点,
∴BE=CN,
∴四边形EBCN是平行四边形,
∴EN=BC,
而由题意可知,可得BC=$\sqrt{(\frac{12}{2})^{2}+(\frac{16}{2})^{2}}$=10,
∴EN=10,
∴PM+PN的最小值为10.
故答案为:10.
点评 考查菱形的性质和轴对称及平行四边形的判定等知识的综合应用.综合运用这些知识是解决本题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
10.种植草莓大户张华现有22吨草莓等待出售,有两种销售渠道,一是运往省城直接批发给零售商,二是在本地市场零售,受客观因素影响,张华每天只能采用一种销售渠道,而且草莓必须在10天内售出(含10天).经过调查分析,这两种销售渠道每天销量及每吨所获纯利润见下表:
(1)若一部分草莓运往省城批发给零售商,其余在本地市场零售,请写出销售22吨草莓所获纯利润y(元)与运往省城直接批发零售商的草莓量x(吨)之间的函数关系式;
(2)怎样安排这22吨草莓的销售渠道,才使张华所获纯利润最大?并求出最大纯利润.
| 销售渠道 | 每日销量 (吨) | 每吨所获纯 利润(元) |
| 省城批发 | 4 | 1200 |
| 本地零售 | 1 | 2000 |
(2)怎样安排这22吨草莓的销售渠道,才使张华所获纯利润最大?并求出最大纯利润.
11.如果点P(a,b)在第二象限,那么点Q(-b,-a)在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
12. 如图,现有一个圆心角为90°,半径为12cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥的底面半径为( )
如图,现有一个圆心角为90°,半径为12cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥的底面半径为( )
 如图,现有一个圆心角为90°,半径为12cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥的底面半径为( )
如图,现有一个圆心角为90°,半径为12cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥的底面半径为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | πcm |