题目内容
18.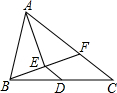 在△ABC中,点D是BC中点,AE平分∠BAC,BE⊥AE于E,延长BE交AC于F.若AB=10厘米,AC=16厘米,则DE=3厘米.
在△ABC中,点D是BC中点,AE平分∠BAC,BE⊥AE于E,延长BE交AC于F.若AB=10厘米,AC=16厘米,则DE=3厘米.
分析 先根据ASA定理得出△ABE≌△AFE,故可得出BE=EF,再根据D为BC中点得出DE是△BCF的中位线,根据三角形的中位线定理即可得出结论.
解答 解:∵AE平分∠BAC,
∴∠BAE=∠CAE.
∵BE⊥AE,
∴∠AEB=∠AEF,
在△ABE与△AFE中,
$\left\{\begin{array}{l}∠BAE=∠FAE\\ AE=AE\\∠AEB=∠AEF\end{array}\right.$,
∴△ABE≌△AFE(ASA),
∴AF=AB,BE=EF.
∵AB=10cm,AC=16cm,
∴AF=10cm,CF=16-10=7cm.
∵D为BC中点,
∴BD=CD.
∴DE是△BCF的中位线,
∴DE=$\frac{CF}{2}$=3cm.
故答案为:3.
点评 本题考查的是三角形中位线定理,熟知三角形的中位线平行于第三边,并且等于第三边的一半是解答此题的关键.

练习册系列答案
相关题目
6. 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )| A. | a>0 | B. | b>0 | C. | c<0 | D. | a+b+c<0 |
8.在3、-5、0、2这四个数中,最小的一个数是( )
| A. | 3 | B. | -5 | C. | 0 | D. | 2 |
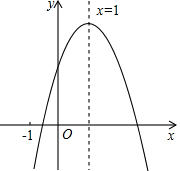 二次函数y=ax2+bx+c的图象如图所示,有下列4个结论:
二次函数y=ax2+bx+c的图象如图所示,有下列4个结论: 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则ac>0.(填“>”、“=”或“<”)
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则ac>0.(填“>”、“=”或“<”)