题目内容
3.在△ABC和△A′B′C′中,∠A,∠B,∠C的对边分别为a,b、c,∠A′,∠B′,∠C′的对边为a′,b′、c′,∠C=∠C′,b-a=b′-a′,b+a=b′+a′,请判断△ABC和△A′B′C′是否全等?答:不一定全等,你的根据是∠C和∠C′不是a、b和a′,b′的夹角,因此不一定全等.分析 首先根据b-a=b′-a′,b+a=b′+a′可得$\left\{\begin{array}{l}{a=a′}\\{b=b′}\end{array}\right.$,然后再根据全等三角形的判定定理可得△ABC和△A′B′C′不一定全等.
解答 解:∵$\left\{\begin{array}{l}{b-a=b′-a′}\\{b+a=b′+a′}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=a′}\\{b=b′}\end{array}\right.$,
∵∠C=∠C′,∠C和∠C′不是a、b和a′,b′的夹角,
∴△ABC和△A′B′C′不一定全等,
故答案为:不一定全等,∠C和∠C′不是a、b和a′,b′的夹角,因此不一定全等.
点评 此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
14.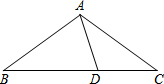 如图,在△ABC中,AB=AC,∠BAC=108°,点D在BC上,且BD=AB,连接AD,则∠CAD等于( )
如图,在△ABC中,AB=AC,∠BAC=108°,点D在BC上,且BD=AB,连接AD,则∠CAD等于( )
 如图,在△ABC中,AB=AC,∠BAC=108°,点D在BC上,且BD=AB,连接AD,则∠CAD等于( )
如图,在△ABC中,AB=AC,∠BAC=108°,点D在BC上,且BD=AB,连接AD,则∠CAD等于( )| A. | 30° | B. | 36° | C. | 38° | D. | 45° |
13.将抛物线y=x2向下平移1个单位,再向左平移2个单位后,所得新抛物线的表达式是( )
| A. | y=(x-1)2+2 | B. | y=(x-2)2+1 | C. | y=(x+1)2-2 | D. | y=(x+2)2-1 |
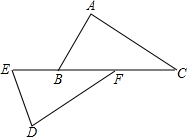 如图,已知E,B,F,C在同一直线上,∠A=∠D,AB=DE,要使△ABC≌△DEF,还需要添加的一个条件是AC=DF.(写出一个即可)
如图,已知E,B,F,C在同一直线上,∠A=∠D,AB=DE,要使△ABC≌△DEF,还需要添加的一个条件是AC=DF.(写出一个即可)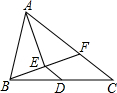 在△ABC中,点D是BC中点,AE平分∠BAC,BE⊥AE于E,延长BE交AC于F.若AB=10厘米,AC=16厘米,则DE=3厘米.
在△ABC中,点D是BC中点,AE平分∠BAC,BE⊥AE于E,延长BE交AC于F.若AB=10厘米,AC=16厘米,则DE=3厘米.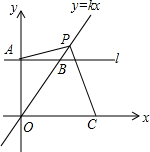 如图,直线l∥x轴,交y轴于点A(0,2),交直线y=kx(k>0)于点B,点P是线段OB延长线上一定,连接AP,过点P作PC⊥AP交x轴于点C.
如图,直线l∥x轴,交y轴于点A(0,2),交直线y=kx(k>0)于点B,点P是线段OB延长线上一定,连接AP,过点P作PC⊥AP交x轴于点C.