题目内容
13．一个正多边形的边长为2cm，它的一个外角是60°，则这个正多边形的面积是6$\sqrt{3}$cm2．分析 多边形的外角和等于360°，因为所给多边形的每个外角均相等，据此即可求得正多边形的边数，进而求解．
解答 解：正多边形的边数是：360÷60=6．
正六边形的边长为2cm，
由于正六边形可分成六个全等的等边三角形，
且等边三角形的边长与正六边形的边长相等，
所以正六边形的面积=6×$\frac{1}{2}$×sin60°×22=6$\sqrt{3}$cm2．
故答案是：6$\sqrt{3}$．
点评 本题考查了正多边形的外角和以及正多边形的计算，正六边形可分成六个全等的等边三角形，转化为等边三角形的计算．
练习册系列答案
阅读快车系列答案
相关题目
如图，从A处到B处，选择第②条路最近．理由是两点之间，线段最短．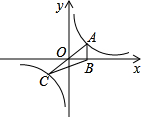
如图，正比例函数y=kx（k＞0）与反比例函数y=$\frac{4}{x}$的图象相交于A、C两点，过点A作x轴的垂线交x轴于点B，连接BC，则△ABC的面积等于4．
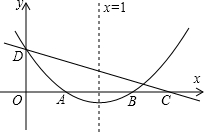如图，直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点，抛物线与x轴交于AB两点，其对称轴为直线x=1，且OA=OD，直线y=kx+c与x轴交于点C（点C在点B的右侧）．则下列命题中正确的个数是（ ）
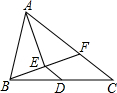在△ABC中，点D是BC中点，AE平分∠BAC，BE⊥AE于E，延长BE交AC于F．若AB=10厘米，AC=16厘米，则DE=3厘米．