题目内容
6. 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )| A. | a>0 | B. | b>0 | C. | c<0 | D. | a+b+c<0 |
分析 根据开口方向、对称轴、抛物线与y轴的交点,确定a、b、c的符号,根据对称轴和图象确定y>0或y<0时,x的范围,确定代数式的符号
解答 解:①∵开口向下,∴a<0,A错误;
②对称轴在y轴的右侧和a<0,可知b>0,B正确;
③抛物线与y轴交于正半轴,c>0,C错误;
④当x=1时,y=0,∴a+b+c=0,D错误;
故选:B.
点评 本题考查的是二次函数图象与系数的关系,掌握二次函数的性质、灵活运用数形结合思想是解题的关键,解答时,要熟练运用抛物线上的点的坐标满足抛物线的解析式.

练习册系列答案
相关题目
14.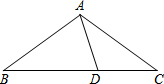 如图,在△ABC中,AB=AC,∠BAC=108°,点D在BC上,且BD=AB,连接AD,则∠CAD等于( )
如图,在△ABC中,AB=AC,∠BAC=108°,点D在BC上,且BD=AB,连接AD,则∠CAD等于( )
 如图,在△ABC中,AB=AC,∠BAC=108°,点D在BC上,且BD=AB,连接AD,则∠CAD等于( )
如图,在△ABC中,AB=AC,∠BAC=108°,点D在BC上,且BD=AB,连接AD,则∠CAD等于( )| A. | 30° | B. | 36° | C. | 38° | D. | 45° |
16.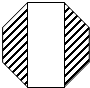 如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )
如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )
 如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )
如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )| A. | $10\sqrt{2}$ | B. | 20 | C. | 18 | D. | $20\sqrt{2}$ |
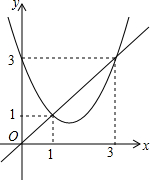 二次函数y=x2+bx+c与直线y=x的图象如图所示,有以下结论:
二次函数y=x2+bx+c与直线y=x的图象如图所示,有以下结论: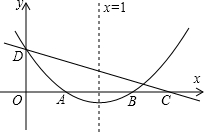 如图,直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点,抛物线与x轴交于AB两点,其对称轴为直线x=1,且OA=OD,直线y=kx+c与x轴交于点C(点C在点B的右侧).则下列命题中正确的个数是( )
如图,直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点,抛物线与x轴交于AB两点,其对称轴为直线x=1,且OA=OD,直线y=kx+c与x轴交于点C(点C在点B的右侧).则下列命题中正确的个数是( )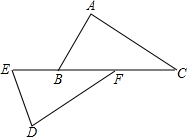 如图,已知E,B,F,C在同一直线上,∠A=∠D,AB=DE,要使△ABC≌△DEF,还需要添加的一个条件是AC=DF.(写出一个即可)
如图,已知E,B,F,C在同一直线上,∠A=∠D,AB=DE,要使△ABC≌△DEF,还需要添加的一个条件是AC=DF.(写出一个即可)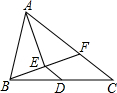 在△ABC中,点D是BC中点,AE平分∠BAC,BE⊥AE于E,延长BE交AC于F.若AB=10厘米,AC=16厘米,则DE=3厘米.
在△ABC中,点D是BC中点,AE平分∠BAC,BE⊥AE于E,延长BE交AC于F.若AB=10厘米,AC=16厘米,则DE=3厘米.