题目内容
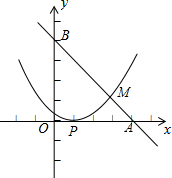 已知,如图,直线l经过A(4,0)和B(0,4)两点,抛物线y=a(x-h)2的顶点为P(1,0),直线l与抛物线的交点为M.
已知,如图,直线l经过A(4,0)和B(0,4)两点,抛物线y=a(x-h)2的顶点为P(1,0),直线l与抛物线的交点为M.(1)求直线l的函数解析式;
(2)若S△AMP=3,求抛物线的解析式.
考点:二次函数的性质,待定系数法求一次函数解析式,待定系数法求二次函数解析式
专题:
分析:(1)设出函数解析式为y=kx+b,利用待定系数法解答即可;
(2)根据三角形的面积求出M点的纵坐标,代入直线解析式求出M的横坐标,再利用P、M的值求出函数解析式.
(2)根据三角形的面积求出M点的纵坐标,代入直线解析式求出M的横坐标,再利用P、M的值求出函数解析式.
解答:解:(1)设一次函数解析式为y=kx+b,
把A(4,0),B(0,4)分别代入解析式得
,
解得
,
解析式为y=-x+4.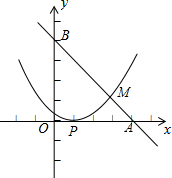
(2)设M点的坐标为(m,n),
∵S△AMP=3,
∴
(4-1)n=3,
解得,n=2,
把M(m,2)代入为2=-m+4得,m=2,
M(2,2),
∵抛物线y=a(x-h)2的顶点为P(1,0),
可得y=a(x-1)2,
把M(2,2)代入y=a(x-1)2得,2=a(2-1)2,解得a=2,函数解析式为y=2(x-1)2.
把A(4,0),B(0,4)分别代入解析式得
|
解得
|
解析式为y=-x+4.
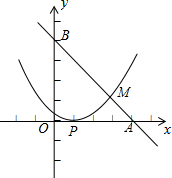
(2)设M点的坐标为(m,n),
∵S△AMP=3,
∴
| 1 |
| 2 |
解得,n=2,
把M(m,2)代入为2=-m+4得,m=2,
M(2,2),
∵抛物线y=a(x-h)2的顶点为P(1,0),
可得y=a(x-1)2,
把M(2,2)代入y=a(x-1)2得,2=a(2-1)2,解得a=2,函数解析式为y=2(x-1)2.
点评:本题考查了二次函数的性质和待定系数法求二次函数解析式、求一次函数解析式,要熟练运用二次函数与一次函数与坐标的特点.

练习册系列答案
相关题目
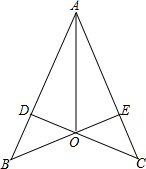 如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O,∠BAO=∠CAO,求证:OB=OC.
如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O,∠BAO=∠CAO,求证:OB=OC.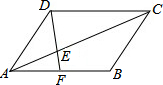 已知如图,在平行四边形ABCD中CE=2AE,DE的延长线交AB于F,求证:AF=FB.
已知如图,在平行四边形ABCD中CE=2AE,DE的延长线交AB于F,求证:AF=FB.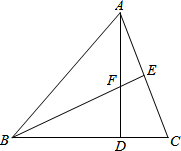 已知,△ABC中,AB=CB,AD⊥BC于D,AD=BD,CD=FD,BF的延长线交AC于E.求证:
已知,△ABC中,AB=CB,AD⊥BC于D,AD=BD,CD=FD,BF的延长线交AC于E.求证: