题目内容
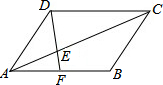已知如图，在平行四边形ABCD中CE=2AE，DE的延长线交AB于F，求证：AF=FB．考点：相似三角形的判定与性质,平行四边形的性质
专题：证明题
分析：根据平行四边形的性质得出AB=CD，AB∥CD，根据相似三角形的判定推出△AEF∽△CED，得出比例式，代入求出即可．
解答：证明：∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，
∴△AEF∽△CED，
∴
=
，
∵AB=CD，CE=2AE，
∴
=
，
∵AF+BF=AB，
∴AF=FB．
∴AB=CD，AB∥CD，
∴△AEF∽△CED，
∴
| AE |
| CE |
| AF |
| DC |
∵AB=CD，CE=2AE，
∴
| AF |
| AB |
| 1 |
| 2 |
∵AF+BF=AB，
∴AF=FB．
点评：本题考查了平行四边饿形的性质，相似三角形的性质和判定的应用，解此题的关键是推出△AEF∽△CED．
练习册系列答案
教学练新同步练习系列答案
相关题目
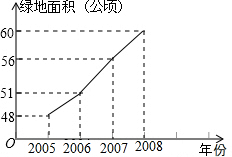某城区近几年通过拆迁旧房，植草，栽树，修建公园等措施，使城区绿地面积不断增加．
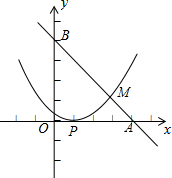已知，如图，直线l经过A（4，0）和B（0，4）两点，抛物线y=a（x-h）2的顶点为P（1，0），直线l与抛物线的交点为M．