题目内容
8. 如图,在等腰梯形ABCD中,AD∥BC,点E、F分别是BD、BC的中点,已知AD=6,BC=12,EF=4,则梯形ABCD的周长为( )
如图,在等腰梯形ABCD中,AD∥BC,点E、F分别是BD、BC的中点,已知AD=6,BC=12,EF=4,则梯形ABCD的周长为( )| A. | 26 | B. | 30 | C. | 32 | D. | 34 |
分析 先证明EF是△BCD的中位线,由三角形中位线定理得出DC=2EF=8,由等腰梯形的性质得出AB=DC=8,梯形ABCD的周长=AB+BC+DC+AD,即可得出结果.
解答 解:∵点E、F分别是BD、BC的中点,
∴EF是△BCD的中位线,
∴DC=2EF=8,
∵四边形ABCD是等腰梯形,
∴AB=DC=8,
∴梯形ABCD的周长=AB+BC+DC+AD=8+12+8+6=34;
故选:D.
点评 本题考查了等腰梯形的性质、三角形中位线定理、梯形周长的计算;熟练掌握等腰梯形的性质和三角形中位线定理是解决问题的关键.

练习册系列答案
相关题目
19. 如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )
如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )
 如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )
如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )| A. | SSS | B. | AAS | C. | SAS | D. | HL |
20.九边形的外角和是( )
| A. | 1 620度 | B. | 1 440度 | C. | 720度 | D. | 360度 |
17.等腰三角形的一个角是50°,则它顶角的度数是( )
| A. | 80°或50° | B. | 80° | C. | 80°或65° | D. | 65° |
18. 如图所示,河对岸有水塔CD.今在A处测得塔顶C的仰角为30°,前进20米到达B处,又测得C的仰角为45°,则塔高CD(精确到0.1m)是( )m.
如图所示,河对岸有水塔CD.今在A处测得塔顶C的仰角为30°,前进20米到达B处,又测得C的仰角为45°,则塔高CD(精确到0.1m)是( )m.
 如图所示,河对岸有水塔CD.今在A处测得塔顶C的仰角为30°,前进20米到达B处,又测得C的仰角为45°,则塔高CD(精确到0.1m)是( )m.
如图所示,河对岸有水塔CD.今在A处测得塔顶C的仰角为30°,前进20米到达B处,又测得C的仰角为45°,则塔高CD(精确到0.1m)是( )m.| A. | 25.3 | B. | 26.3 | C. | 27.3 | D. | 28.3 |
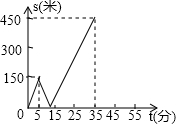 甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙出发沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数函数图象的一部分如图所示,下列说法:
甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙出发沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数函数图象的一部分如图所示,下列说法: 如图,在正方形ABCD的外部作等边三角形△PDC,连结AP、BP,AP交CD于E,BP交CD于F
如图,在正方形ABCD的外部作等边三角形△PDC,连结AP、BP,AP交CD于E,BP交CD于F 关于x的不等式x-2a≤-3的解集如图所示,则a的值是1.
关于x的不等式x-2a≤-3的解集如图所示,则a的值是1.