题目内容

观察下列各式：(a-1)(a+1)=a2-1，(a-1)(a2+a+1)=a3-1，(a-1)(a3+a2+a+1)=a4-1…根据前面各式的规律计算：(a-1)(a4+a3+a2+a+1)=_____；22012+22011+…+22+2+1=_____．

a5-1 22013-1 【解析】观察题目中所给的算式可得(a-1)(a4+a3+a2+a+1)= a5-1； 22012+22011+…+22+2+1 =（2-1）（22012+22011+…+22+2+1） =2×（22012+22011+…+22+2+1）-（22012+22011+…+22+2+1） =22013+22012+22011+…+22+2-2201...
练习册系列答案
相关题目

如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是（　　）

A. 乙前4秒行驶的路程为48米

B. 在0到8秒内甲的速度每秒增加4米/秒

C. 两车到第3秒时行驶的路程相等

D. 在4至8秒内甲的速度都大于乙的速度

C 【解析】试题分析：A．根据图象可得，乙前4秒行驶的路程为12×4=48米，正确； B．根据图象得：在0到8秒内甲的速度每秒增加4米秒/，正确； C．根据图象可得两车到第3秒时行驶的路程不相等，故本选项错误； D．在4至8秒内甲的速度都大于乙的速度，正确； 故选C．

如图，将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上．如果∠2=60°，那么∠1的度数为（　　）

A. 60° B. 50° C. 40° D. 30°

D 【解析】先根据直角三角板的性质得出∠AFE的度数，再根据平行线的性质求出∠2的度数即可． 【解析】 如图所示， ∵△GEF是含45°角的直角三角板， ∴∠GFE=45°， ∵∠1=25°， ∴∠AFE=∠GEF﹣∠1=45°﹣25°=20°， ∵AB∥CD， ∴∠2=∠AFE=20°． 故选C．

如图,已知AE=AD,AB=AC,EC=DB,下列结论:

①∠C=∠B;②∠D=∠E;③∠EAD=∠BAC;④∠B=∠E.其中错误的是(　　)

A. ①② B. ②③ C. ③④ D. 只有④

D 【解析】因为AE＝AD，AB＝AC，EC＝DB； 所以△ABD≌△ACE(SSS)； 所以∠C＝∠B，∠D＝∠E，∠EAC=∠DAB； 所以 ∠EAC-∠DAC=∠DAB-∠DAC； 得∠EAD=∠CAB． 所以错误的结论是④，故选D.

如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘 数”．如：4＝22-02，12＝42-22，20＝62-42，因此4，12，20这三个数都是神秘数．

(1)28和2012这两个数是神秘数吗?为什么?

(2)设两个连续偶数为2k+2和2k(其中k取非负整数)，由这两个连续偶数构造的神秘数是4的倍数吗?为什么?

(3)两个连续奇数的平方差(取正数)是神秘数吗?为什么?

(1)28和2012都是神秘数 (2)这两个连续偶数构造的神秘数是4的倍数(3)两个连续奇数的平方差不是神秘数． 【解析】试题分析： （1）将神秘数4开始，将一些神秘数写成如下的形式4=2×2＝22-02，12＝2×6＝42-22，20＝2×10＝62-42，…，则可判断28和2012这两个数是不是神秘数； （2）将这两个数平方相减，判断它们的差是不是4的倍数； （3）用n...

(x-y+z)（__________）＝z2-( x-y)2．

z-x+y 【解析】∵z2-( x-y)2=(z+x-y)(z-x+y),∴(x-y+z) (z-x+y) ＝z2-( x-y)2．

等边△ABC中，点E在AB上，点D在CA的延长线上，且ED=EC．试探索以下问题：

（1）如图1，当E为AB中点时，试确定线段AD与BE的大小关系，请你直接写出结论：AD BE；

（2）如图2，若点E为线段AB上任意一点，（1）中结论是否成立，若成立，请证明结论，若不成立，请说明理由。

（1）AD=BE；（2）证明见解析 【解析】分析：(1)根据题意易得∠D=∠AED=30°,即可得AD=AE,再根据AE=BE,即可解题; (2)通过作EF∥AC构造等边三角形把BE转化为EF,再利用“角角边”易证△AED≌△FCE,可得AD=FE,即可解题. 本题解析： （1）AD=BE； （2）过点E作EF∥AC交BC于点F， ∴∠EFB=∠ACB，∠BEF...

圆的面积S与半径R之间的关系式是S=πR2，其中自变量是______．

R 【解析】根据函数的定义：对于函数中的每个值R，变量S按照一定的法则有一个确定的值S与之对应可知R是自变量，π是常量. 故答案为：R．

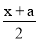已知△ABC的两边长分别为3和7,第三边的长是关于x的方程=x+1的解,求a的取值范围.

6