题目内容
8.从长度分别为1、3、5、7的四条线段中任选三条作边,能构成三角形的概率为$\frac{1}{4}$.分析 先画树状图展示所有24种等可能的结果数,再根据三角形三边的关系找出能构成三角形的结果数,然后根据概率公式求解.
解答 解:画树状图为:
共有24种等可能的结果数,其中能构成三角形的结果数为6,
所以能构成三角形的概率=$\frac{6}{24}$=$\frac{1}{4}$.
故答案为$\frac{1}{4}$.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.也考查了三角形三边的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知关于x的一元二次方程x2-ax-1=0(其中a为常数)的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 可能有实数根,也可能没有实数根 | ||
| C. | 有两个不相等的实数根 | D. | 没有实数根 |
 如图,直线AB、CD、EF相交于O,∠1=40°,∠2=60°,则∠3=80°.
如图,直线AB、CD、EF相交于O,∠1=40°,∠2=60°,则∠3=80°.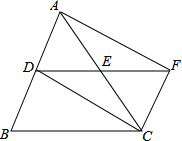 如图,△ABC中,DE是一条中位线,延长DE到点F,使EF=DE,连接CF.
如图,△ABC中,DE是一条中位线,延长DE到点F,使EF=DE,连接CF.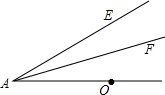 如图,AF平分∠OAE,M是射线AF上一动点,N是线段AO上一动点,判断是否存在点M、N.使得OM+NM的值最小?若存在,请画出M、N点,并加以说明:若不存在,请说明理由.
如图,AF平分∠OAE,M是射线AF上一动点,N是线段AO上一动点,判断是否存在点M、N.使得OM+NM的值最小?若存在,请画出M、N点,并加以说明:若不存在,请说明理由. 二次函数y=x2+bx的图象如图,对称轴为x=-2.若关于x的一元二次方程x2+bx-t=0(t为实数)在-5<x<2的范围内有解,则t的取值范围是-4≤t<12.
二次函数y=x2+bx的图象如图,对称轴为x=-2.若关于x的一元二次方程x2+bx-t=0(t为实数)在-5<x<2的范围内有解,则t的取值范围是-4≤t<12.