题目内容
19.若有理数x,y满足|y-2013|+|x-2|=0(1)求$-\frac{1}{2}xy$的值;
(2)将数y减去它的$\frac{1}{x}$,再减去余下的$\frac{1}{x+1}$,再减去余下的$\frac{1}{x+2}$,再减去余下的$\frac{1}{x+3}$,再减去余下的$\frac{1}{x+4}$,依此类推,直到最后减去余下的$\frac{1}{x+2011}$,求最后所得结果.
分析 首先利用非负数的性质得出x、y的数值.
(1)代入求得数值即可;
(2)根据题意代入,找出规律计算即可.
解答 解:∵有理数x,y满足|y-2013|+|x-2|=0
∴x=2,y=2013,
(1)$-\frac{1}{2}xy$=-2013;
(2)由题意得:
2013×(1-$\frac{1}{2}$)×(1-$\frac{1}{3}$)×(1-$\frac{1}{4}$)×(1-$\frac{1}{5}$)×…×(1-$\frac{1}{2013}$)
=2013×$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$×$\frac{4}{5}$×…××$\frac{2012}{2013}$
=1.
点评 此题考查代数式求值,非负数的性质,有理数的混合运算,利用非负数的性质求得x、y的值是解决问题的前提,利用数据的特点,找出规律是正确计算的关键.

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
9.如图图案是我国几家银行的标志,其中轴对称图形有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
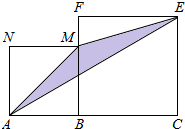 如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为S3;…;当AB=n时,△AME的面积记为Sn,则Sn=$\frac{1}{2}$n2.(用含n的代数式表示)
如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为S3;…;当AB=n时,△AME的面积记为Sn,则Sn=$\frac{1}{2}$n2.(用含n的代数式表示)