题目内容
12.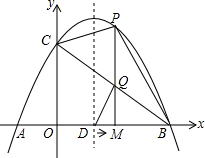 如图,抛物线与x轴交于A、B,与y轴交于C,且OA=1,OB=OC=3,抛物线的对称轴与x轴交于D,点M从O出发,以每秒1个单位长度的速度向B运动到B点止,过M作x轴的垂线交抛物线于点P,交BC于点Q
如图,抛物线与x轴交于A、B,与y轴交于C,且OA=1,OB=OC=3,抛物线的对称轴与x轴交于D,点M从O出发,以每秒1个单位长度的速度向B运动到B点止,过M作x轴的垂线交抛物线于点P,交BC于点Q(1)求这个抛物线的解析式;
(2)设M点运动了x秒时,△BCP的面积为S,求S关于x的函数关系式,并求当S最大时,点P的坐标;
(3)当M点运动多长时间时,△DBQ是等腰三角形?
分析 (1)根据OA=1,OB=OC=3得出A、B、C三点的坐标,再用待定系数法求解即可;
(2)${S}_{△BCP}=\frac{1}{2}({x}_{B}-{x}_{C})×({y}_{P}-{y}_{Q})$;由于B、C坐标已知,所以只需表示出P、Q两点的纵坐标之差即可,而P、Q、M三点的横坐标相同,因此,设出M点的横坐标,将P、Q两点的纵坐标用横坐标表示,这样就把△BCP的面积表示成了关于M点的横坐标的二次函数,配方即可求出最大值,同时可求出P点坐标;
(3)分三种情况分别讨论:DB=DQ;BD=BQ;QB=QD.
解答 解:(1)∵OA=1,OB=OC=3,
∴A(-1,0),B(3,0),C(0,3),
设抛物线的解析式为y=a(x+1)(x-3),
将C点的坐标代入解析式可得:a=-1,
∴抛物线的解析式为:y=-x2+2x+3;
(2)∵B(3,0),C(0,3),
∴BC的解析式为y=-x+3,
设M点的坐标为(m,0),则P(m,-m2+2m+3),Q(m,-m+3),
∴S=${S}_{△BCP}=\frac{1}{2}({x}_{B}-{x}_{C})×({y}_{P}-{y}_{Q})$=$\frac{3}{2}×(-{m}^{2}+2m+3+m-3)$=$-\frac{3}{2}{m}^{2}+\frac{9}{2}m$=$--\frac{3}{2}{(m-\frac{3}{2})}^{2}+\frac{27}{8}$,
∴当m=$\frac{3}{2}$,${S}_{max}=\frac{27}{8}$,
此时,P点的坐标为($\frac{3}{2}$,$\frac{15}{4}$);
(3)∵y=-x2+2x+3=4-(x-1)2+4,
∴D(1,4),
∴BD=2.
设运动时间为t,则M(t,0),则Q(t,-t+3),QM=-t+3;
①若DB=DQ,如图1,
则MD=1-t,
MD2+QM2=QD2,
即:(1-t)2+(-t+3)2=4,
解得:t=1或t=3(舍去);
②若BD=BQ,如图2,
则$\frac{QM}{QB}=\frac{OC}{BC}$,
即:$\frac{-t+3}{2}=\frac{3}{3\sqrt{2}}$,
解得:t=3-$\sqrt{2}$;
③若QB=QD,如图3,
则BM=$\frac{1}{2}BD=1$,
$\frac{QM}{MB}=\frac{OC}{OB}$,
即:$\frac{-t+3}{1}=\frac{3}{3}$,
解得:t=2;
综上所述:当M运动时间为:1秒、(3-$\sqrt{2}$)秒、2秒时,△DBQ是等腰三角形.
点评 本题主要考查了待定系数法求二次函数解析式、三角形面积的坐标表示法、配方法求二次函数最值、等腰三角形的性质、相似三角形的判定与性质、解一元二次方程等多个知识点,有一定综合性,难度适中.第(2)问与第(3)问是高频考点,要引起高度重视,并熟练掌握这类问题的处理技巧.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案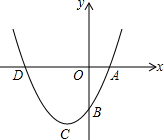 如图,已知抛物线y=x2+bx+c的图象过点A(1,0),B(0,-3).
如图,已知抛物线y=x2+bx+c的图象过点A(1,0),B(0,-3).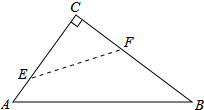 如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上),给出以下判断:
如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上),给出以下判断: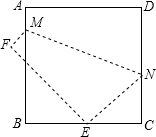 如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN.
如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN.