题目内容
1．已知a，b互为倒数，c，d互为相反数，x的绝对值是1，求x2-（c+d+ab）x-ab的值．分析 根据倒数、相反苏、绝对值的性质可知：ab=1，c+d=0，x=±1，然后代入计算即可．
解答 解：∵a，b互为倒数，c，d互为相反数，x的绝对值是1，
∴ab=1，c+d=0，x=±1．
当x=1时，原式=1-1-1=-1；
当x=-1时，原式=1+1-1=1．
综上所述，代数式x2-（c+d+ab）x-ab的值为±1．
点评 本题主要考查的是求代数式的值，根据题意得到ab=1，c+d=0，x=±1是解题的关键．
练习册系列答案
中考利剑中考试卷汇编系列答案
相关题目
10．下列计算正确的是（ ）
| A． | $\sqrt{8}-\sqrt{2}=\sqrt{6}$ | B． | $\frac{{\sqrt{27}-\sqrt{12}}}{3}=\sqrt{9}-\sqrt{4}$=1 | C． | $（2-\sqrt{5}）（2+\sqrt{5}）=1$ | D． | $\frac{{6-\sqrt{2}}}{{\sqrt{2}}}=3\sqrt{2}$-1 |
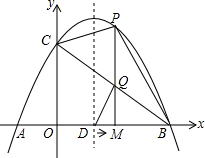如图，抛物线与x轴交于A、B，与y轴交于C，且OA=1，OB=OC=3，抛物线的对称轴与x轴交于D，点M从O出发，以每秒1个单位长度的速度向B运动到B点止，过M作x轴的垂线交抛物线于点P，交BC于点Q
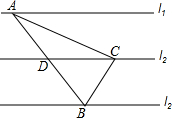已知，如图，直线l1，l2，l3是三条等距的平行线，将一块含30°角的直角三角板如图放置，使直角顶点C落在l2上，另两个顶点A与B刚好分落在l1与l3上，AB与l2交于点D
10．
如图，数轴上点N表示的数可能是（ ）
如图，数轴上点N表示的数可能是（ ）| A． | $\sqrt{10}$ | B． | $\sqrt{6}$ | C． | $\sqrt{3}$ | D． | $\sqrt{2}$ |
