题目内容
将牌面数字分别为1,2,3,4的四张扑克牌背面向上,洗匀后放在桌面上.
(1)从中随机摸出一张牌,牌面数字是偶数的概率是 ;
(2)从中随机摸出两张牌,两张牌牌面数字的和是5的概率是 ;
(3)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法,求出所组成的两位数恰好是3的倍数的概率.
(1)从中随机摸出一张牌,牌面数字是偶数的概率是
(2)从中随机摸出两张牌,两张牌牌面数字的和是5的概率是
(3)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法,求出所组成的两位数恰好是3的倍数的概率.
考点:列表法与树状图法,概率公式
专题:
分析:(1)由题意可知2,4为偶数,由此可求出牌面数字是偶数的概率;
(2)求出所有两张牌的组合,再找到两张牌牌面数字的和是5的个数,进而可求出其概率;
(3)依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率即可.
(2)求出所有两张牌的组合,再找到两张牌牌面数字的和是5的个数,进而可求出其概率;
(3)依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率即可.
解答:解:(1)∵2,4为偶数,
∴从中随机摸出一张牌,牌面数字是偶数的概率=
=
,
故答案为:
;
(2)因为一次抽出两张牌的组合共有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),六种情况,和是5的有2种,
∴从中随机摸出两张牌,两张牌牌面数字的和是5的概率=
;
故答案为:
;
(3)列表如下:
∴P(3的倍数)=
=
.
∴从中随机摸出一张牌,牌面数字是偶数的概率=
| 2 |
| 4 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
(2)因为一次抽出两张牌的组合共有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),六种情况,和是5的有2种,
∴从中随机摸出两张牌,两张牌牌面数字的和是5的概率=
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
(3)列表如下:
| 第二次 第一次 | 1 | 2 | 3 | 4 |
| 1 | 11 | 12 | 13 | 14 |
| 2 | 21 | 22 | 23 | 24 |
| 3 | 31 | 32 | 33 | 34 |
| 4 | 41 | 42 | 43 | 44 |
| 6 |
| 16 |
| 3 |
| 8 |
点评:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
 将两个全等的直角三角形,拼成一个四边形.问:这些四边形中有几个轴对称图形,有几个中心对称图形?
将两个全等的直角三角形,拼成一个四边形.问:这些四边形中有几个轴对称图形,有几个中心对称图形? 在Rt△ABC中,∠C=90°,点D为BC边上一点,CD=1,且cos∠ADC=
在Rt△ABC中,∠C=90°,点D为BC边上一点,CD=1,且cos∠ADC=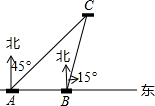 如图,某日我国某岛附近海域有两艘自西向东航行的海监船A、B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)
如图,某日我国某岛附近海域有两艘自西向东航行的海监船A、B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号) 泗州塔,又名西山塔,位于广东惠州西湖的西上之巅,是惠州著名的旅游景点之一.小明运用所学的数学知识对塔进行测量,测量方法如图所示.他在A处测得塔尖D的仰角为45°,再沿AC方向前进20m到达山脚B处,测得塔尖D的仰角为60°,塔底E的仰角为30°,求塔DE的高.(结果精确到0.1m,参考数据:
泗州塔,又名西山塔,位于广东惠州西湖的西上之巅,是惠州著名的旅游景点之一.小明运用所学的数学知识对塔进行测量,测量方法如图所示.他在A处测得塔尖D的仰角为45°,再沿AC方向前进20m到达山脚B处,测得塔尖D的仰角为60°,塔底E的仰角为30°,求塔DE的高.(结果精确到0.1m,参考数据:
 如图,D为锐角△ABC边AC延长线上一点,DF⊥AB于F交BC于E,要使△CED为等腰三角形,则△ABC的边必须满足的条件是
如图,D为锐角△ABC边AC延长线上一点,DF⊥AB于F交BC于E,要使△CED为等腰三角形,则△ABC的边必须满足的条件是