题目内容
7. 如图,在△ABC中,AB=AC,AD⊥BC于D点,点E、F是线段AD上的三等分点,连接BE、CE、BF、CF,若$\frac{BC}{AD}=\frac{2}{3}$,且BC=4a.
如图,在△ABC中,AB=AC,AD⊥BC于D点,点E、F是线段AD上的三等分点,连接BE、CE、BF、CF,若$\frac{BC}{AD}=\frac{2}{3}$,且BC=4a.(1)求四边形ABEC的面积;
(2)写出与△CEF相似但不全等的三角形,并证明其中的一对.
分析 (1)根据等腰三角形的性质三线合一证得BD=CD=$\frac{1}{2}BC=2a$,由点E、F是线段AD上的三等分点,得到DE=EF=AF=$\frac{1}{3}AD$,由于$\frac{BC}{AD}=\frac{2}{3}$,BC=4a,得到DE=EF=AF=2a,根据轴对称的性质得出结论.
(2)根据两边对应成比例且夹角相等,两三角形相似证得结论.
解答 解:(1)∵AB=AC,AD⊥BC,
∴BD=CD=$\frac{1}{2}BC=2a$,
∵点E、F是线段AD上的三等分点,
∴DE=EF=AF=$\frac{1}{3}AD$,
∵$\frac{BC}{AD}=\frac{2}{3}$,BC=4a,
∴DE=EF=AF=2a,
∴由轴对称性可知${S_{四边形ABEC}}=2{S_{△ACE}}=8{a^2}$;
(2)△CAE和△BAE.
由(1)得DE=2a,
∴$CE=2\sqrt{2}a$,
∴CE2=8a2,
∵AE•EF=8a2,
∴AE•EF=CE2,即$\frac{AE}{CE}=\frac{CE}{EF}$,
∵∠AEC=∠CEF,
∴△CEF∽△AEC.
点评 本题考查了等腰三角形的性质三线合一,轴对称的性质,相似三角形的判定,能利用轴对称的性质是解题的关键.

练习册系列答案
相关题目
12. 如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为( )
如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为( )
 如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为( )
如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为( )| A. | 6m2 | B. | 21m2 | C. | 3m2 | D. | 5m2 |
 设函数y1=(x-k)2+k和y2=(x+k)2-k的图象相交于点A,函数y1,y2的图象的顶点分别为B和C.
设函数y1=(x-k)2+k和y2=(x+k)2-k的图象相交于点A,函数y1,y2的图象的顶点分别为B和C.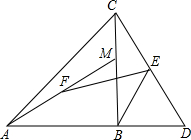 如图,在等腰直角△ABC中,AB=BC,点M是BC边上任意一点,点D是AB的延长线上一点,且BM=BD;又有点E、F分别是CD、AM边的中点,连结FE、EB.下列结论一定正确的有( )
如图,在等腰直角△ABC中,AB=BC,点M是BC边上任意一点,点D是AB的延长线上一点,且BM=BD;又有点E、F分别是CD、AM边的中点,连结FE、EB.下列结论一定正确的有( )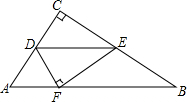 如图,△ABC中,∠C=90°,AC=6,BC=8,D、E分别在AC、BC上且DE∥AB,将△ABC沿DE折叠,使C点落在斜边AB上的F处,则AF的长是( )
如图,△ABC中,∠C=90°,AC=6,BC=8,D、E分别在AC、BC上且DE∥AB,将△ABC沿DE折叠,使C点落在斜边AB上的F处,则AF的长是( )