题目内容
解方程组:
.
|
考点:高次方程
专题:
分析:由①2得:x2•y2=9③,由②、③知:x2、y2分别是方程λ2-10λ+9=0的两个根,求得λ的值,即可解决问题.
解答:解:
由①2得:x2•y2=9③,
由②、③知:
x2、y2分别是方程λ2-10λ+9=0的两个根,
解得λ=1或9;
∴x2=1,y2=9或x2=9,y2=1,
∴原方程组的解为:
,
,
,
.
|
由①2得:x2•y2=9③,
由②、③知:
x2、y2分别是方程λ2-10λ+9=0的两个根,
解得λ=1或9;
∴x2=1,y2=9或x2=9,y2=1,
∴原方程组的解为:
|
|
|
|
点评:该题主要考查了高次方程的解法问题;解题的一般策略是化高次方程为低次方程,化无理方程为有理方程;而常用的方法是换元或平方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,直线l与⊙O相切于A,弦BC交半径OA于D,GB⊥BC交l于G,若OA=R,AD=a,AC=b,则DG=
如图,直线l与⊙O相切于A,弦BC交半径OA于D,GB⊥BC交l于G,若OA=R,AD=a,AC=b,则DG= 小芳的爸爸得了高血压,小芳每天下午5:00放学后都要帮爸爸测量一次血压,如表是小芳的爸爸周一至周五血压的变化情况,他上个周日的血压为162单位.
小芳的爸爸得了高血压,小芳每天下午5:00放学后都要帮爸爸测量一次血压,如表是小芳的爸爸周一至周五血压的变化情况,他上个周日的血压为162单位.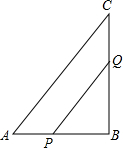 如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始,沿AB边向点B以每秒1cm的速度移动,点Q从点B开始,沿着BC边向点C以每秒2cm的速度移动,如果P、Q同时出发,问:经过几秒钟△PBQ的面积最大?最大面积是多少?
如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始,沿AB边向点B以每秒1cm的速度移动,点Q从点B开始,沿着BC边向点C以每秒2cm的速度移动,如果P、Q同时出发,问:经过几秒钟△PBQ的面积最大?最大面积是多少?