题目内容
1.一组按规律排列的式子:3a2、5a5、7a10、9a17、11a26…,则第n个式子是(2n+1)a${\;}^{{n}^{2}+1}$(n为正整数).分析 根据观察,可发现规律:系数是(2n+1)次数是(n2+1),可得答案.
解答 解:由3a2、5a5、7a10、9a17、11a26…,得
系数是(2n+1)次数是(n2+1),
第n个式子是(2n+1)a${\;}^{{n}^{2}+1}$,
故答案为:(2n+1)a${\;}^{{n}^{2}+1}$.
点评 本题考查了单项式,观察发现规律系数是(2n+1)次数是(n2+1)是解题关键.

练习册系列答案
相关题目
 如图,⊙O是△ABC的外接圆,CG是直径,CE⊥AB于E,CA=8,CB=12,CE=6,求CG的长.
如图,⊙O是△ABC的外接圆,CG是直径,CE⊥AB于E,CA=8,CB=12,CE=6,求CG的长.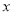 、小明掷B立方体朝上的数字为
、小明掷B立方体朝上的数字为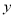 来确定点P(
来确定点P(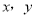 ),那么它们各掷一次所确定的点P落在已知抛物线
),那么它们各掷一次所确定的点P落在已知抛物线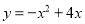 上的概率为( )
上的概率为( )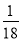 B.
B. 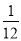 C.
C. 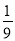 D.
D.