题目内容
12.分式$\frac{|x|-1}{{x}^{2}-x}$,当x≠0或1时有意义;当x=-1时的值为零.分析 根据分式的值为零和分式有意义的条件即可求出x的值.
解答 解:当x2-x≠0时,
即x≠1或x≠0时,
该分式有意义.
当$\left\{\begin{array}{l}{{x}^{2}-x≠0}\\{|x|-1=0}\end{array}\right.$时,
即x=-1时,此时分式的值为0
故答案为:≠0或1;=-1
点评 本题考查分式的值为0以及分式有意的条件,解题的关键是理解两种情况所需要的条件,本题属于基础题型.

练习册系列答案
相关题目
7.下列说法,正确的是( )
| A. | 相等的两个角是对顶角 | |
| B. | 邻补角是互补的两个角,互补的两个角也是邻补角 | |
| C. | 如果两个角有公共顶点和一条公共边,那么它们互为邻补角 | |
| D. | 两条直线相交,如果它们所成的邻补角相等,那么一对对顶角也互补 |
4.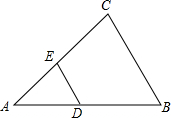 如图,在△ABC中,已知DE∥BC,$\frac{AE}{EC}$=$\frac{2}{3}$,则△ADE与△ABC的周长之比为( )
如图,在△ABC中,已知DE∥BC,$\frac{AE}{EC}$=$\frac{2}{3}$,则△ADE与△ABC的周长之比为( )
 如图,在△ABC中,已知DE∥BC,$\frac{AE}{EC}$=$\frac{2}{3}$,则△ADE与△ABC的周长之比为( )
如图,在△ABC中,已知DE∥BC,$\frac{AE}{EC}$=$\frac{2}{3}$,则△ADE与△ABC的周长之比为( )| A. | 2:3 | B. | 3:2 | C. | 2:5 | D. | 4:25 |
 如图,在Rt△ABC中,∠ACB=90°,CH⊥AB于点H,若BC=5,AC=12,则AB=13,CH=$\frac{60}{13}$.
如图,在Rt△ABC中,∠ACB=90°,CH⊥AB于点H,若BC=5,AC=12,则AB=13,CH=$\frac{60}{13}$. 实数x在数轴上的位置如图所示,试化简:|x+2|-$\sqrt{(-x)^{2}}$-2$\sqrt{9-6x+{x}^{2}}$.
实数x在数轴上的位置如图所示,试化简:|x+2|-$\sqrt{(-x)^{2}}$-2$\sqrt{9-6x+{x}^{2}}$.