题目内容
 关系•拓展:
关系•拓展:如图,已知正方形ABCD,P为边BC上任意一点,连结AP,把AP绕点P顺时针方向旋转90°,点A对应点为点A1,连接A1C,求∠A1CE的度数.
考点:全等三角形的判定与性质,正方形的性质
专题:
分析:过A1作A1Q⊥BE于点Q,由正方形的性质就可以得出△ABP≌△PA1Q,就有BP=A1Q,AB=PQ.,就可以得出PB=CQ,就有A1Q=CQ,就可以求出结论.
解答:解:∠A1CE=45°.
过A1作A1Q⊥BE于点Q,
∴∠A1QP=90°.
∵四边形ABCD是正方形,
∴∠B=90°,AB=BC.
∴∠APB+∠BAP=90°,∠B=∠A1QP.
∵∠APA1=90°,
∴∠APB+∠A1PC=90°,
∴∠BAP=∠A1PC.
在△ABP和△PQA1中,
,
∴△ABP≌△PA1Q(AAS),
∴BP=A1Q,AB=PQ.
∵AB=BC
∴BC-PC=PQ-PC,
∴BP=CQ
∴A1Q=CQ
∴∠A1CE=45°.
过A1作A1Q⊥BE于点Q,
∴∠A1QP=90°.
∵四边形ABCD是正方形,

∴∠B=90°,AB=BC.
∴∠APB+∠BAP=90°,∠B=∠A1QP.
∵∠APA1=90°,
∴∠APB+∠A1PC=90°,
∴∠BAP=∠A1PC.
在△ABP和△PQA1中,
|
∴△ABP≌△PA1Q(AAS),
∴BP=A1Q,AB=PQ.
∵AB=BC
∴BC-PC=PQ-PC,
∴BP=CQ
∴A1Q=CQ
∴∠A1CE=45°.
点评:本题考查了正方形的性质的性质的运用,直角三角形的性质的运用,全等三角形的判断及性质的运用,等式的性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目


 (1)如图,矩形ONEF的对角线交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为
(1)如图,矩形ONEF的对角线交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为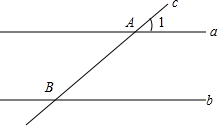 如图,直线a∥b,直线与直线a、b分别交与点A、B且∠1=45°.
如图,直线a∥b,直线与直线a、b分别交与点A、B且∠1=45°.