Question

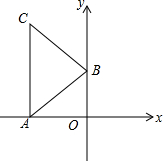
1．在平面直角坐标系xOy中，点A的坐标为（-4，0），点B的坐标为（0，b），将线段BA绕点B顺时针旋转90°得到线段BC，连接AC．
（1）当点B在y轴的正半轴上时，在图1中画出△ABC并求点C的坐标（用含b的式子表示）；
（2）画图探究：当点B在y轴上运动且满足-2≤b≤5时，相应的点C的运动路径形成什么图形．
①在图2中画出该图形；
②描述该图形的特征．

Answer 1

分析 （1）如图，作CM⊥y轴于M．先证明△ABO≌△BCM，推出BO=CM=b，OA=BM=4，推出OM=4+b，由此即可解决问题．
（2））①因为C（-b，4+b），所以点C在直线y=x+4上，图中的线段HK即为点C的运动轨迹．②点C的运动轨迹是线段HK，线段的两个端点的坐标K（-5，9），H（2，2）．

解答 解：（1）如图，作CM⊥y轴于M．
∵∠CMB=∠ABC=∠AOB=90°，
∴∠ABO+∠CBM=90°，∵∠CBM+∠BCM=90°，'∴∠ABO=∠BCM，
在△ABO和△BCM中，
$\left\{\begin{array}{l}{∠AOB=∠CMB}\\{∠ABO=∠BCM}\\{AB=BC}\end{array}\right.$，
∴△ABO≌△BCM，
∴BO=CM=b，OA=BM=4，
∴OM=4+b，
∴C（-b，4+b），

（2）①∵C（-b，4+b），
∴点C在直线y=x+4上，
图中的线段HK即为点C的运动轨迹．

②点C的运动轨迹是线段HK，线段的两个端点的坐标K（-5，9），H（2，2）．

点评 本题考查作图旋转变换、轨迹、一次函数等知识，解题的关键是发现点C的坐标满足直线y=x+4，由此判断出点C的运动轨迹是线段，本题比较难，属于中考常考题型．