题目内容
9．
如图，水平放着的圆柱形排水管的截面，水深EC=8cm，水面宽AB=24cm，则圆柱形排水管的半径为13cm．
分析 连接OA，根据垂径定理得AE=$\frac{1}{2}$AB=12cm，根据勾股定理即刻得到结论．
解答 
解：连接OA，
∵OC⊥AB，
∴AE=$\frac{1}{2}$AB=12cm，
在Rt△OAE中，AO2=OE2+AE2，
即OA2=（OA-8）2+122，
∴OA=13，
∴圆柱形排水管的半径为13cm，
故答案为：13．
点评 本题主要考查了垂径定理和勾股定理，作出恰当的辅助线，利用定理是解答此题的关键．
练习册系列答案
相关题目
19．某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念，全班共送2450张照片，如果全班有x名同学，根据题意，列出方程为（ ）
| A． | x（x+1）=2450 | B． | x（x-1）=2450 | C． | $\frac{1}{2}$x（x+1）=2450 | D． | $\frac{1}{2}$x（x-1）=2450 |
17．下列各项中，结论正确的是（ ）
| A． | 若a＞0，b＜0，则$\frac{b}{a}$＞0 | B． | 若a＞b，则a-b＞0 | ||
| C． | 若a＜0，b＜0，则ab＜0 | D． | 若a＞b，a＜0，则$\frac{b}{a}$＜0 |
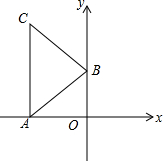在平面直角坐标系xOy中，点A的坐标为（-4，0），点B的坐标为（0，b），将线段BA绕点B顺时针旋转90°得到线段BC，连接AC．
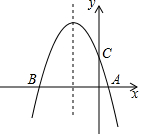如图，抛物线y=-x2+bx+c与x轴交于A（1，0），B（-3，0）两点，与y轴相交于点C，请完成下面的填空：