题目内容
18. 如图,已知菱形ABCD的对角线交于点O,DB=4,AC=8$\sqrt{2}$,求菱形的边长.
如图,已知菱形ABCD的对角线交于点O,DB=4,AC=8$\sqrt{2}$,求菱形的边长.
分析 先由菱形的性质求出OA、OB,再根据勾股定理求出AB即可.
解答 解:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,OA=$\frac{1}{2}$AC=4$\sqrt{2}$,OB=$\frac{1}{2}$BD=2,AC⊥BD,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{(4\sqrt{2})^{2}+{2}^{2}}$=6,
即菱形ABCD的边长为6.
点评 本题考查了菱形的性质以及勾股定理的运用;熟练掌握菱形的性质,运用勾股定理求出边长是解决问题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
13.学生篮球赛中,小方共打了10场球.他在第6,7,8,9场比赛中分别得了:22,15,12和19分,他的前9场比赛的平均得分y比前5场比赛的平均得分x要高.如果他所参加的10场比赛的平均得分超过18分,请问小方在前5场比赛中,总分可达到的最大值以及小方在第10场比赛中,得分可达到的最小值分别是( )
| A. | 85、26 | B. | 85、27 | C. | 84、29 | D. | 84、28 |
7. 菱形OABC在平面直角坐标系中的位置如图所示,若OA=2,∠AOC=60°,则B点的坐标是( )
菱形OABC在平面直角坐标系中的位置如图所示,若OA=2,∠AOC=60°,则B点的坐标是( )
 菱形OABC在平面直角坐标系中的位置如图所示,若OA=2,∠AOC=60°,则B点的坐标是( )
菱形OABC在平面直角坐标系中的位置如图所示,若OA=2,∠AOC=60°,则B点的坐标是( )| A. | (-1,$\sqrt{3}$) | B. | (-3,$\sqrt{3}$) | C. | (-3,$\sqrt{2}$) | D. | (3,$\sqrt{3}$) |
 如图所示,这是个由小立方体搭成的几何体从上面看的视角,小正方形中的数字表示在该位置的小立方体的个数,请画出从正面看和左面看的视图.
如图所示,这是个由小立方体搭成的几何体从上面看的视角,小正方形中的数字表示在该位置的小立方体的个数,请画出从正面看和左面看的视图.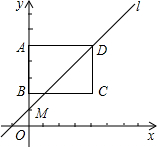 如图,在平面直角坐标系中,矩形ABCD的顶点A、B、C的坐标分别为(0,5)、(0,2)、(4,2),直线l的解析式为y=kx+5-4k(k>0).
如图,在平面直角坐标系中,矩形ABCD的顶点A、B、C的坐标分别为(0,5)、(0,2)、(4,2),直线l的解析式为y=kx+5-4k(k>0).