题目内容
13.学生篮球赛中,小方共打了10场球.他在第6,7,8,9场比赛中分别得了:22,15,12和19分,他的前9场比赛的平均得分y比前5场比赛的平均得分x要高.如果他所参加的10场比赛的平均得分超过18分,请问小方在前5场比赛中,总分可达到的最大值以及小方在第10场比赛中,得分可达到的最小值分别是( )| A. | 85、26 | B. | 85、27 | C. | 84、29 | D. | 84、28 |
分析 设前5场总分为x,然后根据前9场与前5场的平均分的关系列出不等式,然后求解即可;设第10场比赛中得分为y,然后根据10场比赛的平均分列式不等式,然后求解即可.
解答 解:设前5场总分为x,
由题意得,$\frac{x+22+15+12+19}{9}$>$\frac{x}{5}$,
解得x<85,
所以小方在前5场比赛中,总分可达到的最大值是84分;
设第10场比赛中得分为y,
由题意得,$\frac{84+22+15+12+19+y}{10}$>18,
解得:y>28,
所以小方在第10场比赛中,得分可达到的最小值是29分.
故选:C.
点评 本题考查了一元一次不等式的应用,读懂题目信息,找出不等关系然后列出不等式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.下列说法中错误的是( )
| A. | 成轴对称的两个图形的对应点连线的垂直平分线是它们的对称轴 | |
| B. | 关于某条直线对称的两个图形全等 | |
| C. | 若两个图形沿某条直线对折后能够完全重合,我们称两个图形成轴对称 | |
| D. | 全等的三角形一定关于某条直线对称 |
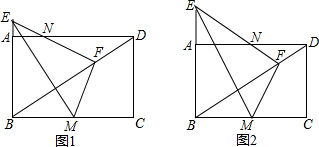
 如图,已知菱形ABCD的对角线交于点O,DB=4,AC=8$\sqrt{2}$,求菱形的边长.
如图,已知菱形ABCD的对角线交于点O,DB=4,AC=8$\sqrt{2}$,求菱形的边长.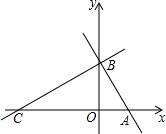 如图,在平面直角坐标系中,已知A(1,0),∠ABO=∠BCO=30°
如图,在平面直角坐标系中,已知A(1,0),∠ABO=∠BCO=30°