题目内容
12.已知一次函数y=kx+b(k≠0)的图象过点(1,-2),则关于x的不等式kx+b+2>0的解集是$\left\{\begin{array}{l}{x<1(k<0)}\\{x>1(k>0)}\end{array}\right.$.分析 分两种情况:①k<0;②k>0;进行讨论可得关于x的不等式kx+b+2>0的解集.
解答 解:∵一次函数y=kx+b(k≠0)的图象过点(1,-2),
∴①k<0时,关于x的不等式kx+b+2>0的解集是x<1;
②k>0时,关于x的不等式kx+b+2>0的解集是x>1.
故关于x的不等式kx+b+2>0的解集是$\left\{\begin{array}{l}{x<1(k<0)}\\{x>1(k>0)}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{x<1(k<0)}\\{x>1(k>0)}\end{array}\right.$.
点评 本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
相关题目
7.下列计算正确的是( )
| A. | x5+x5=x10 | B. | x5•x2=x10 | C. | (x5)5=x10 | D. | (m2)3•m4=m10 |
2.已知x1,x2是方程x2-3x+1=0的两个实数根,则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的值是( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | 1 |
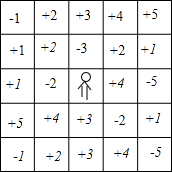 如图是一个“冲出围城”的游戏,规则是:城中人想要冲出围城,可以横走也可以竖走,但不可以斜走,每走一格就可以得到格中相应的分数作为生命值,每格中的分数用乘法累计.当生命值小于+9,并且处于最外圈时,就可以冲出围城,生命值为负数不可以出城.例如:(-2)×(+2)×(+2)×(-1)=+8,就是一条冲出围城的路线.把你找到的冲出围城的路线写下来,也可以直接用箭头将路线在表中表示出来.
如图是一个“冲出围城”的游戏,规则是:城中人想要冲出围城,可以横走也可以竖走,但不可以斜走,每走一格就可以得到格中相应的分数作为生命值,每格中的分数用乘法累计.当生命值小于+9,并且处于最外圈时,就可以冲出围城,生命值为负数不可以出城.例如:(-2)×(+2)×(+2)×(-1)=+8,就是一条冲出围城的路线.把你找到的冲出围城的路线写下来,也可以直接用箭头将路线在表中表示出来.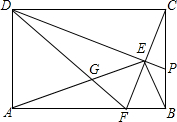 如图所示,在矩形ABCD中.AB=4,BC=3.点F、P分别为线段AB、BC上的动点,CF与DP交于点E,DF与AE交于点G.若GF•DG=AG•GE,连结BE,则BE的最小值为$\sqrt{13}$-2.
如图所示,在矩形ABCD中.AB=4,BC=3.点F、P分别为线段AB、BC上的动点,CF与DP交于点E,DF与AE交于点G.若GF•DG=AG•GE,连结BE,则BE的最小值为$\sqrt{13}$-2.