题目内容
1.“无论多么大的困难除以13亿,都将是一个很小的困难”.在某次特大地震发生后,实验中学全体学生积极参加了“同心协力,抗震救灾”活动,初一年级某班两位同学对本班捐款情况作了统计:两位同学分别绘制了频数分布直方图和扇形统计图.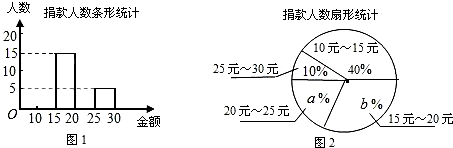
请你根据图中信息,解答下列问题:
(1)这个班的人数是50;
(2)扇形统计图中b=30;
(3)补全频数分布直方图;
(4)扇形统计图中20元到25元组所占圆心角度数是72°.
分析 (1)根据捐款数在25元~30元的有5人,所占的百分比是10%,即可求得总人数;
(2)根据百分比的意义即可求得b的值;
(3)根据百分比的意义求得10元~15元的人数,然后利用总数减去其它各组的人数即可求得20元~25元的人数,从而补全直方图;
(4)利用360°乘以对应的比例即可求得.
解答 解:(1)这个班的人数是:5÷×10%=50(人).
故答案是:50;
(2)b%=$\frac{15}{50}$×100%=30%,则b=30,
故答案是:30;
(3)10元~15元的人数是:50×40%=20(人),
20元~25元的人数是:50-20-15-5=10(人). ;
;
(4)扇形统计图中20元到25元组所占圆心角度数是:360°×$\frac{10}{50}$=72°.
故答案是:72°.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.

练习册系列答案
相关题目
10.关于一元二次方程x2+(4k+1)x+2k-1=0,说法正确的是( )
| A. | 一定有两个相等的实数根 | B. | 一定有实数根 | ||
| C. | 一定有两个不相等的实数根 | D. | 一定没有实数根 |
8. 下列不等式组的解集,在数轴上表示为如图所示的是( )
下列不等式组的解集,在数轴上表示为如图所示的是( )
 下列不等式组的解集,在数轴上表示为如图所示的是( )
下列不等式组的解集,在数轴上表示为如图所示的是( )| A. | $\left\{\begin{array}{l}{x-1>0}\\{x+2≤0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+1>0}\\{x-2≤0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+1≥0}\\{x-2<0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-1≤0}\\{x+2<0}\end{array}\right.$ |
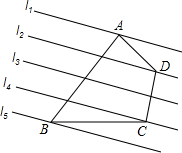 如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=3AD,DC⊥l4,则四边形ABCD的面积是$\frac{17}{2}$.
如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=3AD,DC⊥l4,则四边形ABCD的面积是$\frac{17}{2}$.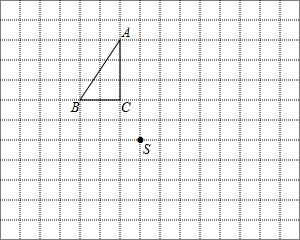 △ABC和点S都在正方形网格的格点上,每个小正方形的边长为1.
△ABC和点S都在正方形网格的格点上,每个小正方形的边长为1.