题目内容
10.计算:(1)|-$\sqrt{\frac{49}{9}}$|-$\root{3}{\frac{64}{27}}$+$\sqrt{(\frac{1}{3})^{2}+(\frac{1}{4})^{2}}$
(2)[(-ab2)2•(-2a2)+$\frac{1}{2}$a3b3+$\frac{1}{4}$a2b2]÷($\frac{1}{2}$ab)2-(-ab-1)2
(3)因式分解:9a2(x-y)+4b2(y-x)
分析 (1)先计算算术平方根、立方根及绝对值、平方,再计算被开方数及其算术平方根,最后计算加法;
(2)先计算单项式的乘方和多项式的乘方,再计算单项式的乘法、多项式除以单项式,最后去括号、合并同类项可得;
(3)先提取公因式x-y,再利用平方差公式分解可得.
解答 解:(1)原式=$\frac{7}{3}$-$\frac{4}{3}$+$\sqrt{\frac{1}{9}+\frac{1}{16}}$
=1+$\sqrt{\frac{16+9}{16×9}}$
=1+$\frac{5}{4×3}$
=1+$\frac{5}{12}$
=$\frac{17}{12}$;
(2)原式=[a2b4•(-2a2)+$\frac{1}{2}$a3b3+$\frac{1}{4}$a2b2]÷($\frac{1}{4}$a2b2)-(a2b2+2ab+1)
=(-2a4b4+$\frac{1}{2}$a3b3+$\frac{1}{4}$a2b2)÷($\frac{1}{4}$a2b2)-(a2b2+2ab+1)
=-8a2b2+2ab+1-a2b2-2ab-1
=-9a2b2;
(3)原式=(x-y)(9a2-4b2)
=(x-y)(3a+2b)(3a-2b).
点评 本题主要考查整式的混合运算、实数的混合运算及因式分解的综合应用,熟练掌握混合运算顺序和运算法则及整式的因式分解是解题的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
18.我市七年级有11000名学生参加期中学业监测,为了了解监测情况,从中抽取2000名学生的成绩进行统计分析,在这个问题中,有下列说法,其中正确的有( )
①2000名学生是总体的一个样本;②11000名学生是总体;③样本容量是2000.
①2000名学生是总体的一个样本;②11000名学生是总体;③样本容量是2000.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
5. 如图,一个长方形观光园,它的长为100米,宽为50米,在它的四角各建一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)花园种植的是花草,设正方形观光休息亭的边长为x米,则下列说法中错误的是( )
如图,一个长方形观光园,它的长为100米,宽为50米,在它的四角各建一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)花园种植的是花草,设正方形观光休息亭的边长为x米,则下列说法中错误的是( )
 如图,一个长方形观光园,它的长为100米,宽为50米,在它的四角各建一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)花园种植的是花草,设正方形观光休息亭的边长为x米,则下列说法中错误的是( )
如图,一个长方形观光园,它的长为100米,宽为50米,在它的四角各建一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)花园种植的是花草,设正方形观光休息亭的边长为x米,则下列说法中错误的是( )| A. | 观光园的周长为300米 | B. | 观光休息亭的占地面积为4x2米2 | ||
| C. | 花园占地面积为(100-2x)(50-2x)米2 | D. | 观光大道总长为(300-2x)米 |
2.下列各式-2a,$\frac{2}{3πb}$,$\frac{1}{a+b}$,$\frac{1}{3}$a2-$\frac{1}{2}$b2,$\frac{π}{2a}$,$\frac{1}{x}$中,分式有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.关于x的二次三项式4x2-kx+9是一个完全平方式,则k的值为( )
| A. | -12 | B. | ±12 | C. | ±6 | D. | 6 |
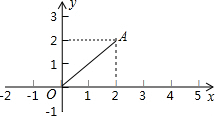 如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P有4个.
如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P有4个.