Question

【题目】已知，点为射线上一点，点为的中点，且.当点在射线上运动时 ，则与和的最小值为_______．

Answer 1

【答案】

【解析】

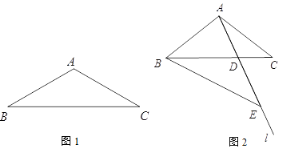
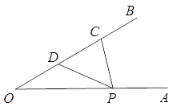
作点D关于OA的对称点D′，连接CD′交OA于点P′，连接DP,，根据轴对称的性质得到P′D′=P′D，此时DP′+CP′=CD′即为PC+PD的最小值，根据已知条件计算求出结果即可．

解：作点D关于OA的对称点D′，连接CD′交OA于点P′，连接DP′，根据轴对称的性质得到P′D′=P′D，此时DP′+CP′=CD′即为PC+PD的最小值.

设DD′与OA交于点E，

∵∠O=30°，OD=3，由对称性可知∠DEO=90°,

∴∠ODE=60°，DE=OD=,

∴DD′=2DE=3,∴DD′=CD，

∴∠D′=∠DCD′=∠ODE=30°，∴∠EDP′=∠D′=30°，

∴∠ODP′=∠ODE+∠EDP′=90°，

∴在Rt△ODP′中，∠O=30°，OD=3，∴DP′=

∴CP′=2DP′=2

∴DP′+CP′=3

故与和的最小值为3