题目内容
【题目】定义:若一个三角形中,其中有一个内角是另外一个内角的一半,则这样的三角形叫做“半角三角形”. 例如:等腰直角三角形就是“半角三角形”.在钝角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 的直线
的直线![]() 交
交![]() 边于点
边于点![]() .点
.点![]() 在直线
在直线![]() 上,且
上,且![]() .
.
(1)若![]() ,点
,点![]() 在
在![]() 延长线上.
延长线上.
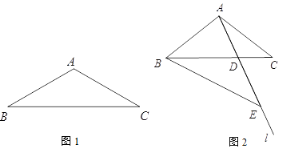
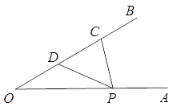
① 当![]() ,点
,点![]() 恰好为
恰好为![]() 中点时,依据题意补全图1.请写出图中的一个“半角三角形”:_______;
中点时,依据题意补全图1.请写出图中的一个“半角三角形”:_______;
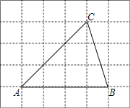
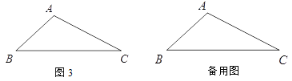
② 如图2,若![]() ,图中是否存在“半角三角形”(△
,图中是否存在“半角三角形”(△![]() 除外),若存在,请写出图中的“半角三角形”,并证明;若不存在,请说明理由;
除外),若存在,请写出图中的“半角三角形”,并证明;若不存在,请说明理由;
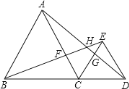
(2)如图3,若![]() ,保持
,保持![]() 的度数与(1)中②的结论相同,请直接写出
的度数与(1)中②的结论相同,请直接写出![]() ,
,![]() ,
,![]() 满足的数量关系:______.
满足的数量关系:______.
【答案】(1)① 如图,见解析;△![]() 或△
或△![]() 或△
或△![]() 或△
或△![]() ; ②存在,“半角三角形”为△
; ②存在,“半角三角形”为△![]() ;证明见解析;(2)
;证明见解析;(2)![]() 或
或![]() .
.
【解析】
(1)①根据题干描述作出图形即可,利用等腰三角形的性质,根据“一个内角是另外一个内角的一半”的三角形符合题意,可得出结果.②延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() ,构造全等三角形△
,构造全等三角形△![]() ≌△
≌△![]() .再利用全等三角形的性质以及相关角度的转化,可求得
.再利用全等三角形的性质以及相关角度的转化,可求得![]() ,从而可得出结果.
,从而可得出结果.
(2)由(1)中②可知,![]() ,延长
,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接BF,构造全等三角形△
,连接BF,构造全等三角形△![]() ≌△
≌△![]() ,进而可得出
,进而可得出![]() .因为
.因为![]() ,所以以
,所以以![]() 为圆心,
为圆心,![]() 长为半径作圆与直线
长为半径作圆与直线![]() 一定有两个交点,当第一种情况成立时,必定存在一个与它互补的
一定有两个交点,当第一种情况成立时,必定存在一个与它互补的![]() ,所以可得出另外一种情况.
,所以可得出另外一种情况.
(1)① 如图,

图中的一个 “半角三角形”:△![]() 或△
或△![]() 或△
或△![]() 或△
或△![]() ;
;
② 存在,“半角三角形”为△![]() .
.
延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() .
.

∵![]() ,
,
∴ ![]() .
.
∴ ![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
在△![]() 和△
和△![]() 中,
中,

∴ △![]() ≌△
≌△![]() .
.
∴ ![]() ,
,![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
∴![]() .
.
∴∠BAE=2∠BEA,
∴△![]() 为“半角三角形”.
为“半角三角形”.
(2)![]() 或
或![]() .
.
解:①延长![]() 到点
到点![]() ,使得
,使得![]() ,连接BF,
,连接BF,

∵![]() ,
,![]() ,
,
∴△![]() ≌△
≌△![]() .
.
过点![]() 分别作
分别作![]() 于点
于点![]() ,
,
![]() 于点
于点![]() ,
,
可得![]() .
.
∴![]() .
.
②因为![]() ,所以以
,所以以![]() 为圆心,
为圆心,![]() 长为半径作圆与直线
长为半径作圆与直线![]() 一定有两个交点,当第一种情况成立时,必定存在一个与它互补的
一定有两个交点,当第一种情况成立时,必定存在一个与它互补的![]() .
.
可知:![]()
综上所述,这三个角之间的关系有两种,
![]() 或
或![]() .
.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案