题目内容
13.(1)计算:$\sqrt{12}-\sqrt{5\frac{1}{3}}-\sqrt{0.27}+\sqrt{\frac{1}{3}}$(2)解方程:(3x-1)2=(x+1)(3x-1)
(3)用配方法解方程:2x2+4x-3=0
(4)分解因式:2x2+4xy-y2.
分析 (1)首先化简二次根式进而合并同类二次根式进而得出答案;
(2)直接利用提取公因式法分解因式,进而解方程得出答案;
(3)利用配方法进行配方得出答案;
(4)首先将y看作常数,进而解方程分解因式即可.
解答 解:(1)$\sqrt{12}-\sqrt{5\frac{1}{3}}-\sqrt{0.27}+\sqrt{\frac{1}{3}}$
=2$\sqrt{3}$-$\sqrt{\frac{16}{3}}$-$\sqrt{\frac{27}{100}}$+$\frac{\sqrt{3}}{3}$
=$\frac{7\sqrt{3}}{3}$-$\frac{4\sqrt{3}}{3}$-$\frac{3\sqrt{3}}{10}$
=$\frac{7\sqrt{3}}{10}$;
(2)(3x-1)2=(x+1)(3x-1)
(3x-1)[3x-1-(x+1)]=0,
解得:x1=$\frac{1}{3}$,x2=1;
(3)2x2+4x-3=0
2x2+4x=3
x2+2x=$\frac{3}{2}$
(x+1)2=$\frac{5}{2}$,
则x+1=±$\frac{\sqrt{10}}{2}$,
解得:x1=-1+$\frac{\sqrt{10}}{2}$,x2=-1-$\frac{\sqrt{10}}{2}$;
(4)2x2+4xy-y2=0,
b2-4ac=16y2-4×2(-y)2=24y2,
x1=$\frac{-4y+2\sqrt{6}y}{4}$=$\frac{-2y+\sqrt{6}y}{2}$,
x2=$\frac{-2y-\sqrt{6}y}{2}$,
则原式=2(x-$\frac{-2y+\sqrt{6}y}{2}$)(x-$\frac{-2y-\sqrt{6}y}{2}$)
=2(x+$\frac{2y-\sqrt{6}y}{2}$)(x+$\frac{2y+\sqrt{6}y}{2}$).
点评 此题主要考查了二次根式的加减运算以及一元二次方程的解法以及实数范围内分解因式,正确解方程是解题关键.

 走进文言文系列答案
走进文言文系列答案| A. | 6x2+x-15 | B. | 3y2+7y+3 | C. | x2+4x+4 | D. | 2x2-4x+5 |
| A. | $\overrightarrow{a}$-$\overrightarrow{b}$=0 | B. | $\overrightarrow{a}$-$\overrightarrow{b}$=$\overrightarrow{b}$-$\overrightarrow{a}$ | ||
| C. | 如果$\overrightarrow{a}$=$\overrightarrow{b}$,那么|$\overrightarrow{a}$|=|$\overrightarrow{b}$| | D. | 如果|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,那么$\overrightarrow{a}$=$\overrightarrow{b}$. |
| A. | -2m | B. | +2m | C. | -5m | D. | +5m |
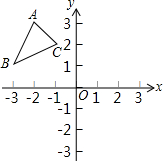 如图,△ABC的三个顶点的坐标分别为A(-2,3),B(-3,1),C(-1,2),分别作出与△ABC关于y轴和x轴对称的图形,并标出各对称点的坐标.
如图,△ABC的三个顶点的坐标分别为A(-2,3),B(-3,1),C(-1,2),分别作出与△ABC关于y轴和x轴对称的图形,并标出各对称点的坐标.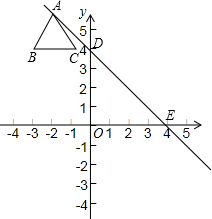 在平面直角坐标系中,直线y=kx+b经过两点D(0,4),E(4,0),边长为2个单位长度的等边△ABC,顶点A在该直线上滑动,在滑动过程中始终保持边BC∥x轴,且顶点A在BC的上方.
在平面直角坐标系中,直线y=kx+b经过两点D(0,4),E(4,0),边长为2个单位长度的等边△ABC,顶点A在该直线上滑动,在滑动过程中始终保持边BC∥x轴,且顶点A在BC的上方.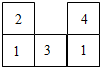 图中是由几个小立方块搭成的几何体的从上面看的形状图,小正方形中的数字表示在该位置的小立方块的个数,请画出这个几何体的从正面看和从左面看的形状图.
图中是由几个小立方块搭成的几何体的从上面看的形状图,小正方形中的数字表示在该位置的小立方块的个数,请画出这个几何体的从正面看和从左面看的形状图.