题目内容
13. (1)已知:如图,点C在线段AB上,线段AC=12,BC=4,点M、N分别是AC、BC的中点,求MN的长度.
(1)已知:如图,点C在线段AB上,线段AC=12,BC=4,点M、N分别是AC、BC的中点,求MN的长度.(2)根据(1)的计算过程与结果,设AC+BC=a,其它条件不变,你能猜出MN的长度吗?请用一句简洁的语言表达你发现的规律.
分析 (1)根据线段中点的性质,可得CM的长,CN的长,根据线段中点的性质,可得答案;
(2)根据线段中点的性质,可得CM的长,CN的长,根据线段中点的性质,可得答案;
解答 解:(1)由点M、N分别是AC、BC的中点,得
MC=$\frac{1}{2}$AC,NC=$\frac{1}{2}$BC.
由线段的和差,得
MN=MC+NC=$\frac{1}{2}$AC+$\frac{1}{2}$BC=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$×(12+4)=8;
(2)由点M、N分别是AC、BC的中点,得
MC=$\frac{1}{2}$AC,NC=$\frac{1}{2}$BC.
由线段的和差,得
MN=MC+NC=$\frac{1}{2}$AC+$\frac{1}{2}$BC=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$a.
规律是:线段上的点把线段分成两条线段,这两条线段中点间的距离是原线段长的一半.
点评 本题考查了两点间的距离,利用线段中点的性质得出MC的长,NC的长是解题关键,又利用了线段的和差.

练习册系列答案
相关题目
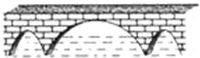 如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的.正常水位时,大孔水面宽度为20m,顶点距水面6m,小孔顶点距水面4.5m.当水位上涨刚好淹没小孔时,大孔的水面宽度为10m.
如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的.正常水位时,大孔水面宽度为20m,顶点距水面6m,小孔顶点距水面4.5m.当水位上涨刚好淹没小孔时,大孔的水面宽度为10m.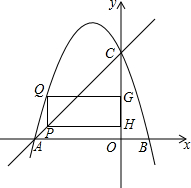 如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(-3,0)、B(1,0),与y轴交于点C.点P为线段AC上一点(不与点A、C重合),PH⊥y轴于点H,PQ∥y轴交抛物线于点Q,QG⊥y轴于点G.设点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(-3,0)、B(1,0),与y轴交于点C.点P为线段AC上一点(不与点A、C重合),PH⊥y轴于点H,PQ∥y轴交抛物线于点Q,QG⊥y轴于点G.设点P的横坐标为m. 如图,已知线段AB,点E、F分别是线段AC、BD的中点,CD=4cm,AC+BD=10cm
如图,已知线段AB,点E、F分别是线段AC、BD的中点,CD=4cm,AC+BD=10cm