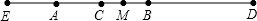题目内容
3. 如图,已知线段AB,点E、F分别是线段AC、BD的中点,CD=4cm,AC+BD=10cm
如图,已知线段AB,点E、F分别是线段AC、BD的中点,CD=4cm,AC+BD=10cm(1)求线段EF的长度;
(2)若CD=a,AC+BD=b,则EF=a$+\frac{1}{2}$b.
分析 (1)根据线段中点的性质得到EC=$\frac{1}{2}$AC,DF=$\frac{1}{2}$BD,结合图形计算即可;
(2)根据线段中点的性质得到EC=$\frac{1}{2}$AC,DF=$\frac{1}{2}$BD,结合图形、代入数据计算即可.
解答 解:(1)∵点E、F分别是线段AC、BD的中点,
∴EC=$\frac{1}{2}$AC,DF=$\frac{1}{2}$BD,
∴EC+DF=$\frac{1}{2}$(AC+BD)=5cm,
∴EF=EC+DF+CD=9cm;
(2)∵点E、F分别是线段AC、BD的中点,
∴EC=$\frac{1}{2}$AC,DF=$\frac{1}{2}$BD,
∴EC+DF=$\frac{1}{2}$(AC+BD)=$\frac{1}{2}$b,
∴EF=EC+DF+CD=a$+\frac{1}{2}$b.
故答案为:a$+\frac{1}{2}$b.
点评 本题考查的是两点间的距离的计算,掌握线段中点的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 将一副三角板按如图所示摆放,则∠ABC的度数为( )
将一副三角板按如图所示摆放,则∠ABC的度数为( )
 将一副三角板按如图所示摆放,则∠ABC的度数为( )
将一副三角板按如图所示摆放,则∠ABC的度数为( )| A. | 70° | B. | 75° | C. | 80° | D. | 85° |
15.计算$\frac{b}{a}$•$\frac{{a}^{2}-a}{b}$的结果是( )
| A. | a+1 | B. | a-1 | C. | ab-1 | D. | ab-b |
13.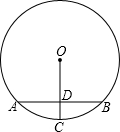 如图,O是圆心,半径OC⊥弦AB于点D,AB=8,OD=3,则CD等于( )
如图,O是圆心,半径OC⊥弦AB于点D,AB=8,OD=3,则CD等于( )
 如图,O是圆心,半径OC⊥弦AB于点D,AB=8,OD=3,则CD等于( )
如图,O是圆心,半径OC⊥弦AB于点D,AB=8,OD=3,则CD等于( )| A. | 2 | B. | 3 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
 (1)已知:如图,点C在线段AB上,线段AC=12,BC=4,点M、N分别是AC、BC的中点,求MN的长度.
(1)已知:如图,点C在线段AB上,线段AC=12,BC=4,点M、N分别是AC、BC的中点,求MN的长度. 根据下面给出的条件,解答下面的问题:(填空)
根据下面给出的条件,解答下面的问题:(填空)